二 次 函 数
一、 重点知识及常用结论1. 二次函数的解析式
(1)一般式:f(x)=ax2+bx+c;
(2)顶点式:f(x)=a(x-h)2+k,(h,k)为顶点;
(3)零点式:f(x)=a(x-x1)(x-x2).
2. 闭区间上的二次函数的最值

二、 典型例题及易错题型
二次函数在高考中常考不衰,特别是二次函数的图像和单调性是高考的常考内容,作为一种基本函数,二次函数除考查在给定区间上的最值(或值域)和三个“二次”之间的关系的应用外,常常与其他函数、不等式、方程等知识在较为综合的题型中出现.
例1 (浙江卷)若函数f(x)=x2+ax+b在区间[0,1]上的最大值是M,最小值是m,则M-m的值 ( )
A. 与a有关,且与b有关 B. 与a有关,但与b无关
C. 与a无关,且与b无关 D. 与a无关,但与b有关

方法突破:解决二次函数在给定区间上的最值的关键是“二点一线”,二点指闭区间的端点,一线指二次函数图像的对称轴.当明确了对称轴与区间的关系,就确定了函数的单调性,进而确定了函数的最值.
例2 (河南安阳二模)函数f(x)=ax2+bx+c,且a>b>c,a+b+c=0,则( )
A. ∃x0∈(0,1),f(x0)=0 B. ∃x0∈(0,1),f(x0)>0
C. ∀x∈(0,1),f(x)>0 D. ∀x∈(0,1),f(x)<0
答案:D 解析:依题意,a>b>c且a+b+c=0,则a>0,c<0,①当b>0时,对称轴为
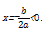 .又f(0)=c<0,f(1)=a+b+c=0,图像如图1所示,则∀x∈(0,1),f(x)<0.
.又f(0)=c<0,f(1)=a+b+c=0,图像如图1所示,则∀x∈(0,1),f(x)<0.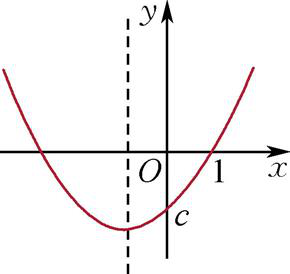
图1
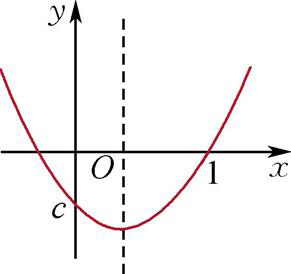
图2
②当b<0时,对称轴为
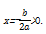 .又f(0)=c<0,f(1)=a+b+c=0,图像如图2所示,则∀x∈(0,1),f(x)<0.
.又f(0)=c<0,f(1)=a+b+c=0,图像如图2所示,则∀x∈(0,1),f(x)<0.综上,∀x∈(0,1),f(x)<0.故选D.
方法突破:与二次函数单调性相关的问题,应结合图像的开口方向以及对称轴的位置进行分析、讨论求解。



发表评论 取消回复