1. 集合的含义
(1)集合与元素的含义一般地,一定范围内某些确定的、不同的对象的全体构成一个集合.集合中的每一个对象称为该集合的元素,简称元.
(2)集合中元素的特性:确定性、无序性、互异性.
2. 元素与集合的关系

3. 常用数集的符号
自然数集N;正整数集N*或N+;整数集Z;有理数集Q;实数集R.4. 集合的表示方法和分类
(1)集合的表示方法:列举法、描述法、Venn图法.(2)集合的分类
①按元素个数分:空集、有限集、无限集;
②按元素特征分:数集、点集.
5. 集合与集合之间的关系

6. 集合与集合之间的运算

7. 函数的概念及表示法


8. 函数的图像
作函数图像的基本方法:(1)描点法.“描点法”的作图步骤:列表、描点、连线.取的点越多,图像越精确.
(2)图像变换法





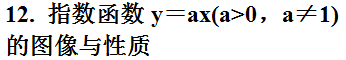







发表评论 取消回复