（8月7日）数学 《高中数学 小题狂作 提优版 必修1》p13第14题 疑惑：解析上说因为f（x）对任意x∈R都有f（1/2+x）+f（1/2-x）等于2，但是其中的f（1/2+x）+f（1/2-x）为什么等于2，您在错题集中说根据题目“关于点（1/2，1）对称”得出来的，能否具体解释一下，我还是不太明白。

编辑解答：

函数对称中有这样的结论：
函数y=f(x)关于点（a，0）对称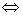对定义域内的任意x都有f(a+x)+f(a-x)=0
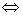对定义域内的任意x都有f(2a-x)+f(x）=0.
由此类推出一般结论：函数y=f(x)关于点（a，b）对称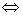对定义域内的任意x都有f(a+x)+f(a-x)=2b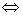对定义域内的任意x都有f(2a-x)+f(x）=2b.
这个结论需要牢记，这对我们解这类函数关于点对称的题目有帮助.