数学知识梳理(必修3)
1. 算法的概念及特征
(1)概念
对一类问题的机械的、统一的求解方法称为算法.找到了某种算法,是指使用一系列运算规则能在有限步骤内求解某问题,其中的每条规则必须是明确定义的、可行的.
(2)特征
有限性:一个算法的步骤是有限的,必须在有限操作之后停止,不能是无限的.
确定性:算法的每一步骤和次序应当是确定的.
有效性:算法的每一步骤都必须是有效的.
2. 程序框图与算法的基本逻辑结构
(1)程序框图又称流程图,是一种用程序框、流程线及文字说明来表示算法的图像.(2)算法的基本逻辑结构
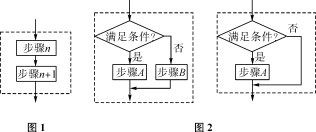
①顺序结构:由若干个依次执行的步骤组成(如图1).
②条件结构:先根据条件作出判断,再决定执行哪一种操作的结构(如图2).
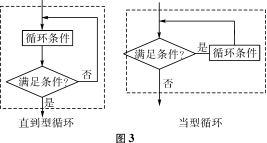
③循环结构:需要重复执行同一操作的结构,分为直到型循环和当型循环(如图3).
3. 基本算法语句

4. 算法案列
辗转相除法与更相减损法、秦九韶算法、进位制.5. 抽样方法
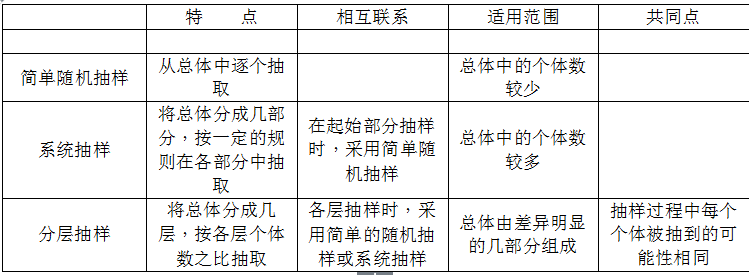
常见的抽样方法有:简单随机抽样(抽签法、随机数法)、系统抽样、分层抽样.三种抽样方法的区别与联系如下表:
6. 用样本估计总体
(1)频率分布表制作频率分布表的步骤:
①求全距.决定组数和组距,组数=组距;
②分组.通常对组内数值所在区间取左闭右开区间,最后一组取闭区间;
③登记频数.计算频率,列出频率分布表.
(2)频率分布直方图与折线图
制作频率分布直方图的步骤:
①先制作频率分布表,然后作直角坐标系;
②把横轴分成若干段,每一线段对应1个组的组距;
③以此线段为底作矩形,它的高等于该组的组距,这样得出一系列的矩形,每个矩形的面积恰好是该组的频率,这些矩形就构成了频率分布直方图.
如果将频率分布直方图中各相邻的矩形的上底边的中点顺次连结起来,那么就得到频率分布折线图,简称频率折线图.
(3)茎叶图:当数据是两位有效数字时,用中间的数字表示十位数,即第一个有效数字,两边的数字表示个位数,即第二个有效数字.它的中间部分像植物的茎,两边像植物茎上长出来的叶子,这种表示数据的图叫做茎叶图.

7. 变量间的相关关系

8. 随机事件及其概率
(1)必然事件、不可能事件、随机事件:必然事件是指在一定条件下必然发生的事件;不可能事件是指在一定条件下不可能发生的事件;随机事件是指在一定条件下可能发生也可能不发生的事件.要辨析清事件的条件和结果,理解事件的结果是相应于“一定条件”而言的,必须明确什么是事件发生的条件,什么是在此条件下产生的结果.上述三种事件都是在一定条件下的结果.
(2)随机事件的概率
一般地,对于给定的随机事件A,在相同条件下,随着试验次数的增加,事件A发生的频率会在某个常数附近摆动并趋于稳定,我们可以用这个常数来刻画随机事件A发生的可能性大小,并把这个常数称为随机事件A的概率,记作P(A).
(3)必然事件的概率为1,不可能事件的概率为0,随机事件的概率:0<P(A)<1,
(4)互斥事件、对立事件
“互斥事件”与“对立事件”都是就两个事件而言的,互斥事件是不可能同时发生的两个事件,而对立事件是其中必有一个发生的互斥事件,因此,对立事件必须是互斥事件,但互斥事件不一定是对立事件,也就是说“互斥”是“对立”的必要不充分的条件.






发表评论 取消回复