全等三角形
知识回放
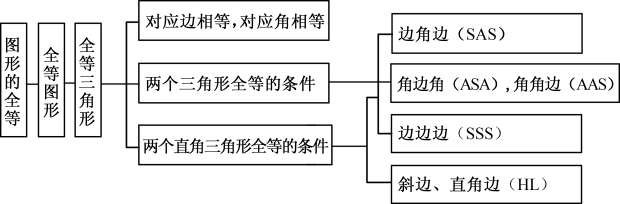
名师精讲
考点一 根据全等三角形性质证明

名师精讲
考点一 根据全等三角形性质证明
例1 (盐城市阜宁县月考)如图1,A、D、E三点在同一直线上,且△BAD≌△ACE.
(1) 求证:BD=DE+CE;
(2) 当△ABD满足什么条件时,BD∥CE?
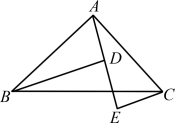 图1
图1解析:(1)根据全等三角形的性质求出BD=AE,AD=CE,代入求出即可;(2)根据全等三角形的性质求出∠E=∠BDA=90°,推出∠BDE=90°,根据平行线的判定求出即可.
解:(1) 因为△BAD≌△ACE,所以BD=AE,AD=CE,所以BD=AE=AD+DE=CE+DE,即BD=DE+CE.
(2) 当△ABD满足∠ADB=90°时,BD∥CE.
理由是:因为△BAD≌△ACE,所以∠E=∠ADB.
若添加的条件∠ADB=90°,则∠E=90°.所以∠BDE=180°-90°=90°=∠E,所以BD∥CE.
点评:解答这一类型问题的基本思路是根据全等三角形的性质得出相等的线段和角,再结合相关几何知识证明结论.
考点二 三角形全等的证明
1. 已知两边对应相等
例2 (泰州市兴化市期中)如图2,C为BE上一点,点A、D分别在BE两侧,AB∥ED,AB=CE,BC=ED,求证:AC=CD.
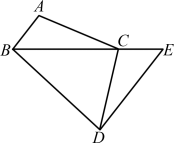 图2
图2
点评:当题目中已给出两组对边相等或经过转化能得出两组对边相等时,若能推出第三条边对应相等,则用“SSS”判定;若能推出两边的夹角相等,则用“SAS”判定.
2. 已知一组边和一组角对应相等
例3 (泰州市期中)如图3,AD与BC相交于点O,∠CAB=∠DBA,AC=BD.求证:△AOC≌△BOD.
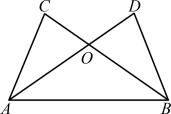 图3
图3解析:题目中已知一角一边相等,且图形中有一公共边AB这个隐含条件,可知AB=BA,从而满足“SAS”.根据已知利用“SAS”判定△ABC≌△BAD得到∠C=∠D,再根据“AAS”判定△AOC≌△BOD.
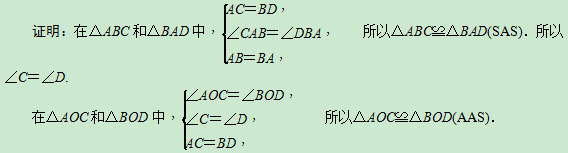
点评:当题目中已给出一组边和一组角对应相等或经过转化能得出这两个条件时,若这组边就是已知角的对边,则只能确定另外一角对应边相等,利用“AAS”判定;若这组边是已知角的一边时,则可寻找已知角的另一边相等,利用“SAS”判定,或找出另外一组相等的对应角,利用“ASA”或“AAS”判定.
3. 已知两组角对应相等
例4 (泰州市姜堰区期中)如图4,四边形ABCD的对角线AC与BD相交于点O,∠1=∠2,∠3=∠4.求证:△ABC≌△ADC.
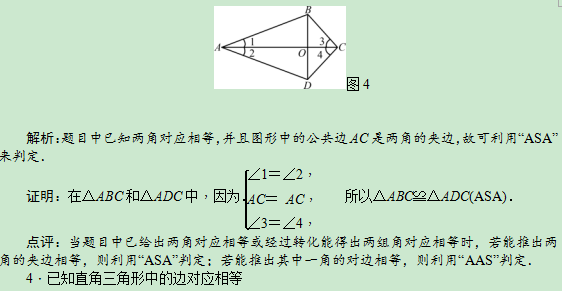

考点三 角平分线的作图
例6 (苏州市虎丘区期中)如图6,已知点D在△ABC的AB边上,且∠ACD=∠A.
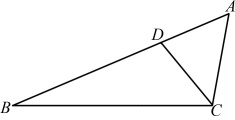 图6
图6(1) 作∠BDC的平分线DE,交BC于点E(用尺规作图法,保留作图痕迹,不要求写作法);
(2) 在(1)的条件下,判断直线DE与直线AC的位置关系.(不要求证明)
解析:(1)根据角平分线基本作图的作法作图即可;(2)根据角平分线的性质可得∠BDE=2∠BDC,根据三角形内角与外角的性质可得∠A=2∠BDC,再根据同位角相等两直线平行可得结论.
解:(1) 如图所示.
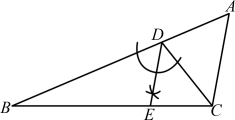 图7
图7(2) DE∥AC.理由是:因为DE平分∠BDC,所以∠BDE=2∠BDC.因为∠ACD=∠A,∠ACD+∠A=∠BDC,所以∠A=2∠BDC,所以∠A=∠BDE,所以DE∥AC.
点评:解答本题的关键是掌握角平分线的作图的一般步骤,再结合角平分线定义和平行线的性质作出判断.
考点四 垂线的作图
例7 (泰州市兴化市期中)如图8,已知线段a、b,求作Rt△ABC,使a为一条直角边,b为一条斜边.(不要求写作法,保留作图痕迹)
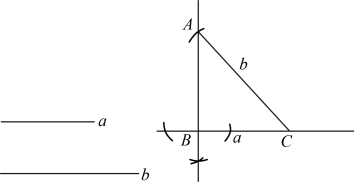 图8 图9
图8 图9 解析:首先画一条直线,在直线上截取BC=a,再过点B作BC的垂线,以C为圆心,b的长为半径画弧,交BC的垂线于点A,连接AC即可.
解:如图9所示,Rt△ABC即为所求.
点评:解答这一类型问题的一般思路是首先根据要求画出草图,再结合草图分析得出画图的步骤,再进行作图.本题解答的关键是熟练掌握做一条直线的垂线的基本作图方法.
临门一脚
本章重点主要是三角形全等的证明,这是证明线段相等、角相等的常用思路,在证明两个三角形全等时,一般先找出已有条件和隐含条件,再寻求需要转化才能得到的间接条件.在一些复杂问题中有时还要添加辅助线构造全等三角形.



发表评论 取消回复