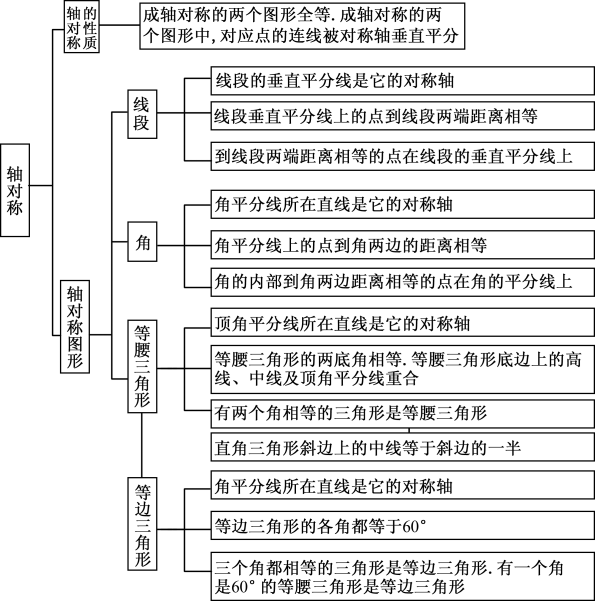
轴对称图形
知识回放

名师精讲
考点一 轴对称图形的识别　
 
例1　(盐城市盐都区期中)在以下永洁环保、绿色食品、节能、绿色环保四个标志中，是轴对称图形的是(　　)
      
解析：A不是轴对称图形，不符合题意；B是轴对称图形，符合题意；C不是轴对称图形，不符合题意；D不是轴对称图形，不符合题意．故选B.
答案：B
点评：确定轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．
考点二 轴对称的性质　
 

例2　(连云港市期中)如图1，△ABC与△DEF关于直线l对称，则∠F等于(　　)
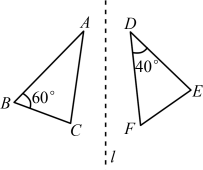图1
 
 
A. 60°  B. 40°  
C. 80°  D. 60°或80°
解析：因为△ABC与△DEF关于直线l对称，所以∠A＝∠D＝40°，∠B＝∠E＝60°，所以∠F＝180°－60°－40°＝180°－100°＝80°.故选C.
答案：C
点评：根据成轴对称的两个图形全等，再根据全等三角形的对应角相等，再结合三角形的内角和定理计算．
考点三 线段的垂直平分线的性质及其判定的运用　

例3　(无锡市江阴市期中)如图2，在△ABC中，AB＝a，AC＝b，BC边上的垂直平分线DE交BC、BA分别于点D、E，求△AEC的周长．
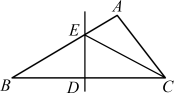图2
 
 
解析：要求三角形的周长，知道AC＝b，只要求得AE＋EC即可，由DE是BC的垂直平分线，结合线段的垂直平分线的性质，知EC＝BE，这样三角形周长的一部分AE＋EC＝AE＋BE＝AB，代入数值，答案可得．
解：因为ED垂直且平分BC，所以BE＝CE.
因为AB＝a，AC＝b，所以AB＝AE＋BE＝AE＋CE＝a，
所以△AEC的周长为AE＋EC＋AC＝a＋b.
点评：本题中三角形的各边长无法直接计算，通过线段的垂直平分线性质将线段转化，再整体求解.
考点四  角平分线性质及其判定的运用　
 
例4　(无锡市期中)如图3，在△ABC中，∠B的平分线BD与∠C的外角平分线CE交于点P.求证：点P到三边AB、BC、CA所在的直线的距离相等．
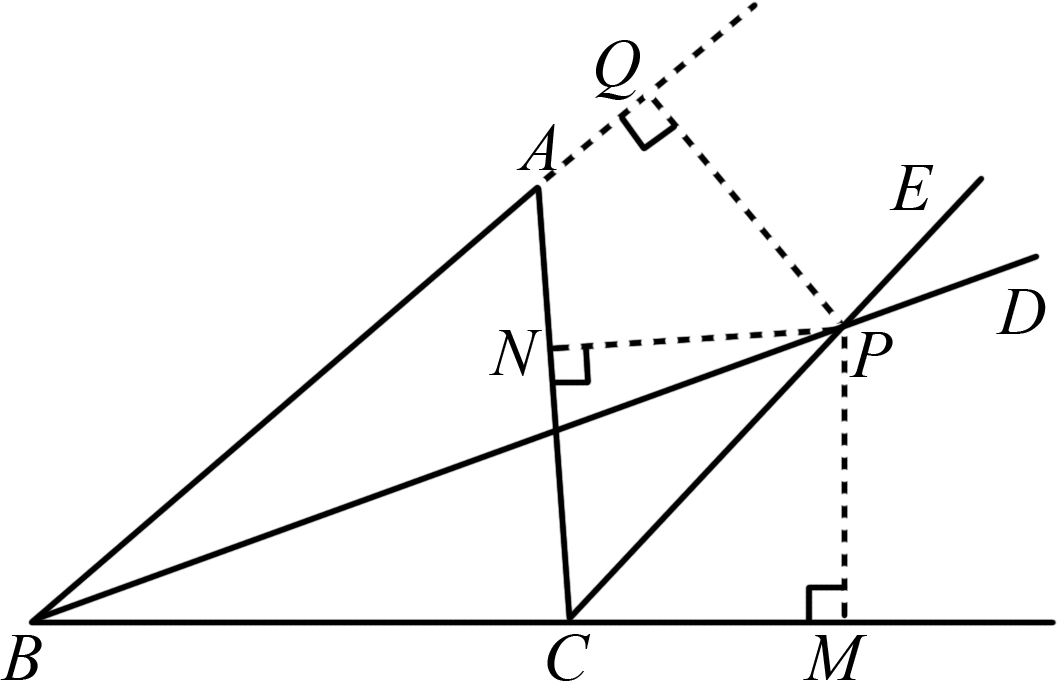图3
 
 
解析：过点P作三边AB、BC、CA所在直线的垂线，垂足分别是Q、M、N.根据角平分线性质即可证明．
证明：如图3，过点P作三边AB、BC、CA所在直线的垂线，垂足分别是Q、M、N.则垂线段PQ、PM、PN，即为点P到三边AB、BC、CA所在直线的距离．
因为P是∠ABC的平分线BD上的一点，所以PM＝PQ.
因为P是∠ACM的平分线CE上的一点，所以PM＝PN.
所以PQ＝PM＝PN.
所以点P到三边AB、BC、CA所在直线的距离相等．
点评：在解答角平分线问题时如果直接解答有困难，通常考虑过角平分线上的点向角的两边作垂线段，构造全等三角形，根据角平分线性质作答．
考点五 角平分线与线段的垂直平分线的作图　
 
例5　(无锡市宜兴市期中)如图4，已知∠AOB及点M、N.
用尺规作图作一点P，使得它到∠AOB两边的距离相等，且到M、N两点的距离也相等．(保留作图痕迹)
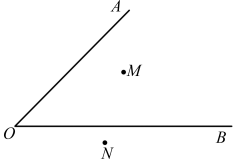图4
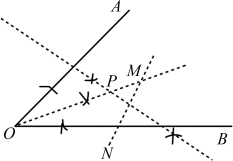　　　图5
 
 
解析：点P到∠AOB两边的距离相等，即在∠AOB的平分线上，点P到M、N两点的距离也相等，即在MN的垂直平分线上，所以作出∠AOB的平分线和MN的垂直平分线，它们的交点为点P.
解：如图5，点P为所求作的点．
点评：解答这类尺规作图问题要注意：①尽量用铅笔作图，作图要按步骤进行，决不徒手画图，草率行事；②要虚实分明，一般辅助性的线用虚线，要求画出的线用实线，要保留作图痕迹．保留作图痕迹才可以体现作图全过程．
考点六 等腰三角形的性质　
 
例6　(无锡市滨湖区期中)如图6，在△ABC中，AB＝AC，AD∥BC，求证：AD平分∠EAC.
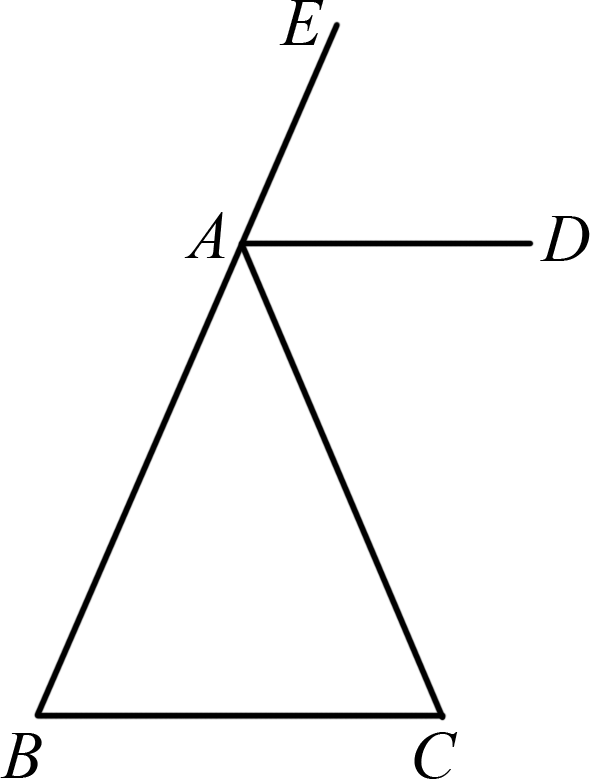图6
 
 
解析：由等边对等角可得到∠B＝∠C，再根据平行线的性质可得到∠EAD＝∠B＝∠C＝∠DAC，即AD平分∠EAC.
证明：因为AB＝AC，
所以∠B＝∠C.
因为AD∥BC，
所以∠EAD＝∠B＝∠C＝∠DAC，
所以AD平分∠EAC.
点评：证明角相等时，如果两个角在同一个三角形中，通常考虑根据“等边对等角”证明．
考点七 等腰三角形的判定　
 
例7　(泰州市姜堰区期中)如图7，在△ABC中，BD、CD分别平分∠ABC、∠ACB，过点D作直线平行于BC，分别交AB、AC于点E、F，求证：EF＝BE＋CF.
解析：根据平行线的性质和角平分线的性质，解出△BED和△CFD是等腰三角形，通过等量代换即可得出结论．
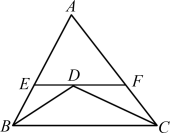图7
 
 
证明：如图8，因为在△ABC中，BD、CD分别平分∠ABC、∠ACB，
所以∠1＝∠2，∠5＝∠6.
因为EF∥BC，所以∠2＝∠3，∠4＝∠6，
所以∠1＝∠3，∠4＝∠5，
所以BE＝ED，DF＝FC，
所以EF＝ED＋DF＝BE＋CF.
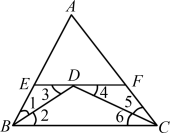图8
 
 
点评：条件中有平行线，有角平行线，通常存在等腰三角形．
考点八 等边三角形的性质及其判定　

例8　(扬州市高邮市期中)如图9，△ABC是等边三角形，点D、E、F分别在线段AB、BC、CA上．
(1) 若AD＝BE＝CF，问△DEF是等边三角形吗？试证明你的结论；
(2) 若△DEF是等边三角形，问AD＝BE＝CF成立吗？试证明你的结论．
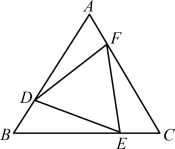图9
 
 
解析：(1)由“SAS”易证△ADF≌△BED≌△CFE，所以DF＝DE＝EF，即△DEF是等边三角形；(2)如图10，先证明∠1＋∠2＝120°，∠2＋∠3＝120°.可得∠1＝∠3.同理∠3＝∠4.则△ADF≌△BED≌△CFE，故能证明AD＝BE＝CF.
解：(1) △DEF是等边三角形．证明如下：
因为△ABC是等边三角形，所以∠A＝∠B＝∠C，AB＝BC＝CA.
又因为AD＝BE＝CF，所以DB＝EC＝FA，
所以△ADF≌△BED≌△CFE，
所以DF＝DE＝EF，即△DEF是等边三角形．
(2) AD＝BE＝CF成立．证明如下：
如图10，因为△DEF是等边三角形，
所以DE＝EF＝FD，∠FDE＝∠DEF＝∠EFD＝60°，
所以∠1＋∠2＝120°.
又因为△ABC是等边三角形，所以∠A＝∠B＝∠C＝60°，
所以∠2＋∠3＝120°，所以∠1＝∠3.
同理∠3＝∠4，所以△ADF≌△BED≌△CFE，所以AD＝BE＝CF.
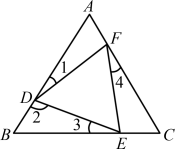图10
 
 
点评：判定等边三角形的常用方法有三种：(1)三边都相等，(2)三个角都是60°，(3)有一个角是60°的等腰三角形是等边三角形．
考点九 直角三角形的性质　
 
例9　(南京市六合区期中)如图11，在四边形ABCD中，∠ABC＝∠ADC＝90°，M是AC的中点．求证：MD＝MB.
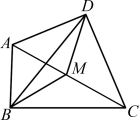图11
 
 
解析：将MD、MB分别置于直角三角形ADC和直角三角形ABC中，然后根据直角三角形的性质(斜边上中线的长度等于斜边的一半)来求证即可．
证明：因为∠ABC＝90°，M是AC的中点，所以BM＝2(1)AC.
同理可证DM＝2(1)AC.
所以DM＝MB.
点评：“直角三角形斜边上的中线等于斜边的一半”这一性质的应用对于不少同学而言是一个难点．认真阅读题意，找出直角和中点，再将图形从复杂的背景中分离出来就可以发现这一结论．
考点十  轴对称图形的设计　
 
例10　(盐城市大丰市期中)已知：图12中①、②均为5×6的正方形网格，点A、B、C在格点(小正方形的顶点)上．请你分别在图①、②中确定格点D，画出一个以A、B、C、D为顶点的四边形，使其为轴对称图形，并画出对称轴．
解析：根据轴对称图形的性质设计出轴对称图形即可．
解：如图12所示．
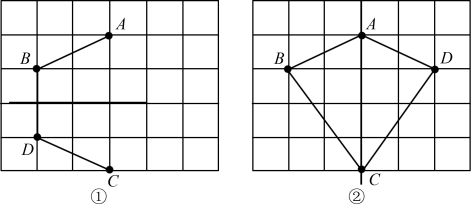图12
 
 
点评：这类网格中轴对称图形的构图解答的基本思路是先确定一条对称轴，一般来说对称轴有两种类型，一种是与网格平行的直线，另外一种是网格所在的正方形的对角线．再根据对称轴补出图形．
临门一脚 
轴对称图形是每年中考重点内容，特别地，等腰三角形的性质及其判定更是考查的重点，解答等腰三角形要注意分类思想的运用，以及三角形常见辅助线的运用．遇到等腰三角形常考虑作底边上的高，即“等腰三角形三线合一”，遇角平分线常考虑向角的两边作垂线段等．同一个三角形中证明角相等常考虑“等边对等角”．