勾股定理
知识回放

名师精讲
考点一 根据勾股定理计算
例1 (南京市鼓楼区期末)如图1,在Rt△ABC中,∠ABC=90°,AB=3,AC=5,点E在BC上,将△ABC沿AE折叠,使点B落在AC边上的点B′处,则BE的长为________.
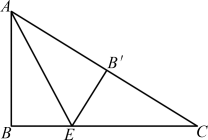 图1
图1
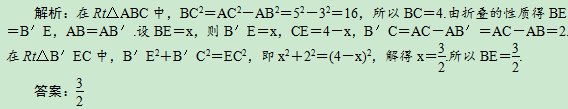
点评:勾股定理说到底是一个等式,而含有未知数的等式就是方程.所以在利用勾股定理求线段的长时,常常利用解方程来解决.勾股定理表达式中有三个量,如果条件中只有一个已知量,必须设法求出另一个量或求出另外两个量之间的关系,这一点是利用勾股定理求线段的长时需要明确的思路.
考点二 根据勾股定理的逆定理计算
例2 (泰州市海陵区期末)如图2,在四边形ABCD中,AB=3 cm,AD=4 cm,BC=13 cm,CD=12 cm,∠A=90°,求四边形ABCD的面积.
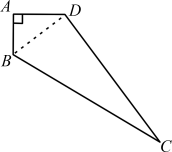 图2
图2
解析:连接BD.
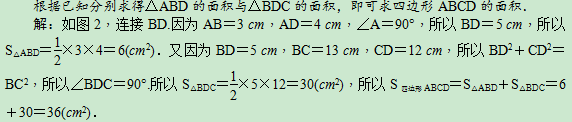
点评:不规则图形的面积计算的基本思路是割补,即将原图形分割或补成可计算图形的面积,本题是将四边形转化为两个三角形计算,但要注意解答本题时要运用勾股定理的逆定理证明∠BDC=90°.
考点三 根据弦图计算

名师精讲
考点一 根据勾股定理计算
例1 (南京市鼓楼区期末)如图1,在Rt△ABC中,∠ABC=90°,AB=3,AC=5,点E在BC上,将△ABC沿AE折叠,使点B落在AC边上的点B′处,则BE的长为________.
 图1
图1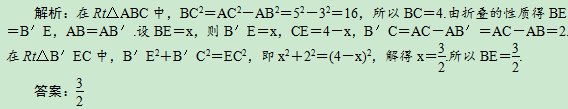
点评:勾股定理说到底是一个等式,而含有未知数的等式就是方程.所以在利用勾股定理求线段的长时,常常利用解方程来解决.勾股定理表达式中有三个量,如果条件中只有一个已知量,必须设法求出另一个量或求出另外两个量之间的关系,这一点是利用勾股定理求线段的长时需要明确的思路.
考点二 根据勾股定理的逆定理计算
例2 (泰州市海陵区期末)如图2,在四边形ABCD中,AB=3 cm,AD=4 cm,BC=13 cm,CD=12 cm,∠A=90°,求四边形ABCD的面积.
 图2
图2解析:连接BD.
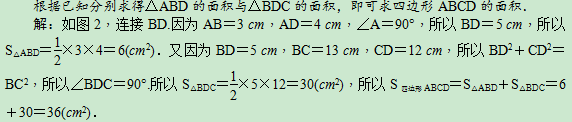
点评:不规则图形的面积计算的基本思路是割补,即将原图形分割或补成可计算图形的面积,本题是将四边形转化为两个三角形计算,但要注意解答本题时要运用勾股定理的逆定理证明∠BDC=90°.
考点三 根据弦图计算
例3 (泰州市兴化市期末)我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成一个大正方形(如图3).如果大正方形的面积是13,小正方形的面积是1,直角三角形的两直角边长分别为a、b,试求(a+b)2 的值.
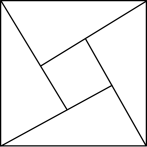 图3
图3解析:根据勾股定理可以求得a2+b2等于大正方形的面积,然后求四个直角三角形的面积,即可得到ab的值,然后根据(a+b)2=a2+2ab+b2即可求解.

点评:关于弦图的计算是中考常考题型,解答这一问题的关键是把握好图形中两个正方形和四个直角三角形之间的关系,再结合完全平方公式计算.
考点四 勾股定理的实际应用
例4 (扬州市宝应县期末)如图4,有两棵树,一棵高12 m,另一棵高6 m,两树相距8 m,一只鸟从一棵树的树梢飞到另一棵树的树梢,那么小鸟至少飞行________m.
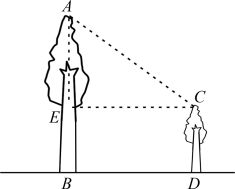 图4
图4
答案:10
点评:运用勾股定理解决问题通常需要作垂线构造直角三角形,再结合勾股定理计算.
临门一脚
勾股定理是数学中的一个重要定理,勾股定理的证明是本章重要内容,也是勾股定理魅力之所在,要重视几种常见的拼图证明勾股定理的方法以及数学思想的运用.要注意勾股定理及其逆定理的联系与区别,学会构造直角三角形运用勾股定理.解勾股定理的实际问题时,通常采用列方程的方法来处理.已知直角三角形的两边求第三边时,应进行分类,以防漏解.求空间图形表面路径最短的问题,一般是将立体图形展开转化为平面图形借助勾股定理求解.



发表评论 取消回复