指数函数、对数函数与幂函数
一、 重点知识及常用结论1. 指数函数y=ax(a>0,a≠1)的图像与性质
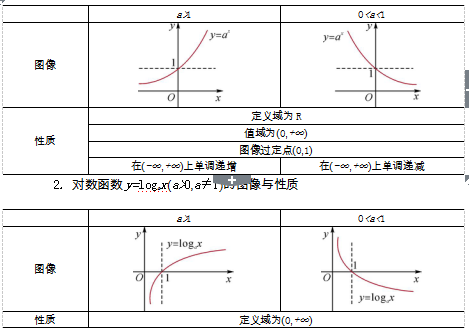

注:指数函数y=ax(a>0且a≠1)与对数函数y=logax(a>0且a≠1)互为反函数,它们的图像关于直线y=x对称.
3. 幂函数y=xα(α∈R)的图像与性质
(1)所有的幂函数在(0,+∞)上有定义,并且图像都过点(1,1).
(2)当α>0时,幂函数的图像通过原点,并且在区间[0,+∞)上是增函数.特别地,当α>1时,幂函数的图像下凸;当0<α<1时,幂函数的图像上凸.
(3)当α<0时,幂函数的图像在区间(0,+∞)上是减函数.在第一象限内,当x从右边趋向原点时,图像在y轴右方无限地逼近y轴正半轴;当x趋于+∞时,图像在x轴上方无限地逼近x轴正半轴.

点拨:中学阶段只要求掌握α=±1,2,3,1/2,1/3这6类,只要把握好幂函数在第一象限内的图像就可以了.
二、 典型例题及易错题型
指数函数、对数函数、幂函数是中学数学中重要的三类基本初等函数,对它们的考查主要集中于图像与性质的考查,同时,也会将它们与其他函数进行复合,从而考查一些复合函数的图像与性质.
例1 (辽宁师大附中期中)设函数f(x)=ln(1+x)-ln(1-x),则f(x)是( )
A. 偶函数,且在(0,1)上是减函数
B. 奇函数,且在(0,1)上是减函数
C. 偶函数,且在(0,1)上是增函数
D. 奇函数,且在(0,1)上是增函数

易错警示:一是在函数的转化过程中,或当研究函数的性质时,一定要注意定义域优先原则,否则容易致错;二是判断复合函数的单调性,要弄清由哪些基本初等函数复合而成,再由“同性为增,异性为减”做出判断.




发表评论 取消回复