导数在研究函数中的应用
一、 重点知识及常用结论1. 导数与函数的单调区间:
①解不等式f'(x)>0得 f(x)的单调递增区间;
②解不等式f'(x)<0得 f(x)的单调递减区间.
2. 利用导数研究函数单调性的相关结论
(1)在区间上f'(x)>0(f'(x)<0)是函数f(x)在此区间上为增(减)函数的充分不必要条件.如果出现个别点使f'(x)=0,不会影响函数f(x)在该区间上的单调性.
(2)如果恒有f'(x)=0,那么函数f(x)在这个区间上是常数函数.
3. 导数与函数的极值
①在函数的定义域内求出方程f'(x)=0的解x0,
②若在x0左侧有f'(x)>0,在x0右侧有f'(x)<0,则f(x)在x=x0取得极大值f(x0).
③若在x0左侧有f'(x)<0,在x0右侧有f'(x)>0,则f(x)在x=x0取得极小值f(x0).
④函数的极值具有不唯一性,即一个函数在某区间上或定义域内的极大值或极小值可能不止一个.且极大值与极小值之间无确定的大小关系.
4. 求函数y=f(x)在[a,b]上的最大值与最小值的步骤:
①求函数y=f(x)在(a,b)上的极值;
②将函数y=f(x)的各极值与端点处的函数值f(a),f(b)比较,其中最大的一个为最大值,最小的一个为最小值.
=二、 典型例题及易错题型
函数的单调性是函数的核心性质,而导数是研究函数的单调性的重要手段,利用导数研究函数的单调性确定极值(或最值)及图像等相关性质,是高考考查的重点内容.
例1 (河南洛阳统考)已知函数f(x)=ex+mlnx(m∈R,e为自然对数的底数).若对任意的正数x1,x2,当x1>x2时,都有f(x1)-f(x2)>x1-x2成立,则实数m的取值范围为 .
答案:[0,+∞) 解析:因为对任意正数x1,x2,当x1>x2时都有f(x1)-f(x2)>x1-x2成立,所以f(x1)-x1>f(x2)-x2成立.g(x)=f(x)-x=ex+mlnx-x,则g(x)在(0,+∞)上单调递增,即g'(x)=ex+m/x-1≥0在(0,+∞)上恒成立,也就是m≥(1-ex)x恒成立,令h(x)=(1-ex)x,则h'(x)=1-ex-xex=1-(1+x)ex,因为x∈(0,+∞),所以ex>1,1+x>1,则h'(x)=1-(1+x)ex<0在(0,+∞)上恒成立,所以h(x)在(0,+∞)上单调递减,所以h(x)<h(0)=0,所以m≥0,即实数m的取值范围是[0,+∞).
方法突破:已知可导函数f(x)在指定的区间D上单调递增(减),求参数范围问题,可转化为f'(x)≥0(或f'(x)≤0)恒成立问题,从而构建不等式,要注意“=”是否可以取到.
例2 (海南八校联考)已知函数f(x)=ex+x2+(3a+2)x在区间(-1,0)上有最小值,则实数a的取值范围是 ( )
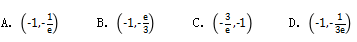
答案:D 解析:因为f'(x)=ex+2x+3a+2,而y=ex和y=2x均在区间(-1,0)上为增函数,所以f'(x)=ex+2x+3a+2在区间(-1,0)上为增函数.又函数f(x)=ex+x2+(3a+2)x在区间(-1,0)上有最小值,所以f'(x)=ex+2x+3a+2在区间(-1,0)上不可能恒正或恒负.因此有
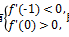 即-
即-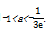
方法突破:求函数在闭区间上的最值和在开区间上的最值的方法不同.求函数在闭区间上的最值,不仅要研究其极值情况,还要研究其单调性,并通过单调性和极值情况,画出函数的大致图像,然后借助图像,比较极值与端点值的大小,观察得到函数的最值。



发表评论 取消回复