导数的概念与运算
一、 重点知识及常用结论1. 导数的几何意义
函数f(x)在x=x0处的导数f'(x0),就是曲线y=f(x)在点(x0,f(x0))处的切线的斜率(如图).
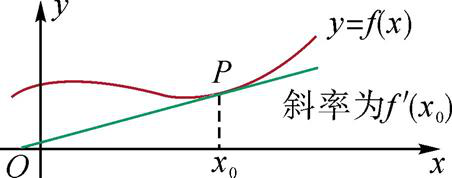
2. 导数的运算
(1)常用求导公式
①C'=0(C为常数);
②(xa)'=axa-1(a为常数且不为0);
③(ex)'=ex;
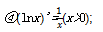
⑤(sinx)'=cosx;
⑥(cosx)'=-sinx.
(2)函数的和、差、积、商的求导法则
①[f(x)±g(x)]'=f'(x)±g'(x);
②[Cf(x)]'=Cf'(x)(C为常数);
③[f(x)g(x)]'=f'(x)g(x)+f(x)g'(x);
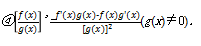
二、 典型例题及易错题型
导数的概念与运算要掌握两个方面的内容:一是关于导数的运算问题,即要熟练地应用相关的导数公式及其运算法则,正确地求解函数的导数;二是掌握函数在某点处的导数的定义、几何意义.
例 过点P(2,-2)和曲线y=3x-x3相切的直线方程为 .

方法突破:曲线的切线与切点有关,当讨论曲线的切线时,缺乏切点信息,需设出切点,通过求导求出切线的斜率,由点斜式方程求出切线方程,再根据题设条件求得切点的坐标,进而完成问题的解答.
易错警示:在求函数的切线时,要注意区别“函数在某点处的切线”与“函数过某点的切线”这两个概念.前者的切线是唯一的,后者的点可以是切点,也可以不是切点,而且切线可能有多条。



发表评论 取消回复