1. 柱、锥、台、球的结构特征
(1)棱柱定义:由一个平面多边形沿某一方向平移形成的空间几何体叫做棱柱。



圆台和球.
2. 空间几何体的三视图
(1)正视图反映了物体上下、左右的位置关系,即反映了物体的高度和长度;
(2)俯视图反映了物体左右、前后的位置关系,即反映了物体的长度和宽度;
(3)侧视图反映了物体上下、前后的位置关系,即反映了物体的高度和宽度.
3. 空间几何体的直观图——斜二测画法

4. 柱体、锥体、台体的表面积与体积
(1)几何体的表面积为几何体各个面的面积的和.(2)柱体、锥体、台体的表面积公式(c为底面周长,h为高,h′为斜高,l为母线)
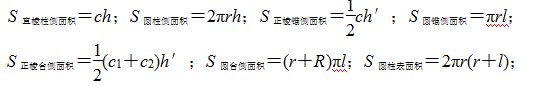

5. 空间点、直线、平面的位置关系


6. 空间中的平行问题
(1)直线与平面平行的判定及其性质
判定定理:平面外一条直线与此平面内一条直线平行,则该直线与此平面平行.
性质定理:如果一条直线和一个平面平行,经过这条直线的任一平面与该平面的交线和该直线平行.
(2)平面与平面平行的判定及其性质
判定定理:如果一个平面内的两条相交直线都平行于另一个平面,那么这两个平面平行.
性质定理:如果两个平行平面都和第三个平面相交,那么它们的交线平行.
7. 空间中的垂直问题
(1)线线、线面、面面垂直的定义①两条异面直线的垂直:如果两条异面直线所成的角是直角,就说这两条异面直线互相垂直.
②线面垂直:如果一条直线和一个平面内的任何一条直线垂直,就说这条直线和这个平面垂直.
③面面垂直:如果两个平面相交,所成的二面角是直二面角,就说这两个平面垂直.
(2)垂直关系的判定和性质定理
①线面垂直判定定理和性质定理
判定定理:如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面.
性质定理:如果两条直线同垂直于一个平面,那么这两条直线平行.
②面面垂直的判定定理和性质定理
判定定理:如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直.
性质定理:如果两个平面互相垂直,那么在一个平面内垂直于它们的交线的直线垂直于另一个平面.
8. 空间角




10. 圆的方程






发表评论 取消回复