有理数
知识回放
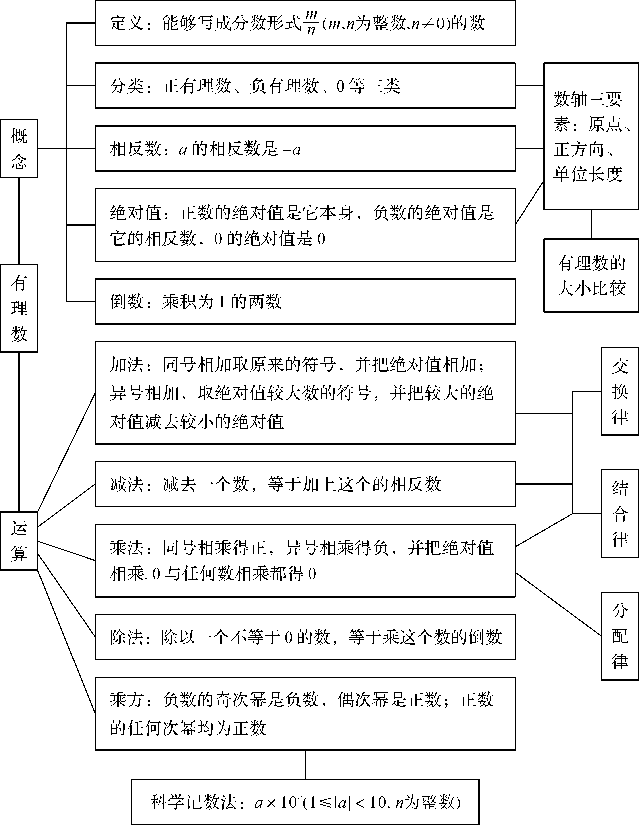
名师精讲
考点一 正负数的意义
例1 选择题:
(1)(盐城市中考)如果收入50元,记作+50元,那么支出30元记作( )
A. +30元 B. -30元 C. +80元 D. -80元
(2)如果水位升高3 m时水位变化记作+3 m,那么水位下降3 m时水位变化记作( )
A. -3 m B. 3 m C. 6 m D. -6 m
解析:首先审清题意,明确“正”和“负”所表示的意义,再根据题意作答.
答案:(1)B (2)A
点评:本题考查了正数和负数,解题关键是理解“正”和“负”的相对性,明确什么是一对具有相反意义的量.在一对具有相反意义的量中,先规定其中一个为正,则另一个就用负表示.
考点二 相反数、绝对值、倒数
例2 填空:
(1)(南京市中考)-2的相反数是________,-2的绝对值是________;

答案:(1)2 2 (2)3
点评:本题主要考查了相反数、绝对值、倒数的定义,要求熟练运用定义解题.
例3 (徐州市中考)点A,B,C在同一条数轴上,其中点A、B表示的数分别为-3、1,若BC=2,则AC等于( )
A. 3 B. 2 C. 3或5 D. 2或6
解析:本题利用数形结合思想,将A,B,C三点在数轴上表示后,即可计算AC的长.又因为题设条件点C的位置未知,故必须对此进行分类讨论,即点C在线段AB内或点C在线段AB外等两种情形.因为点A,B表示的数分别为-3、1,故AB=4.
当点C在线段AB外,如图1所示,AC=4+2=6;
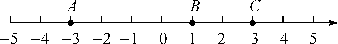 图1
图1
当点C在线段AB内,如图所2示,AC=4-2=2.
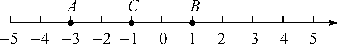 图2
图2
答案:D
点评:根据绝对值的定义可知,在数轴上表示x1,x2的两个数的点A、B之间的距离公式是AB=
考点三 有理数的大小比较

名师精讲
考点一 正负数的意义
例1 选择题:
(1)(盐城市中考)如果收入50元,记作+50元,那么支出30元记作( )
A. +30元 B. -30元 C. +80元 D. -80元
(2)如果水位升高3 m时水位变化记作+3 m,那么水位下降3 m时水位变化记作( )
A. -3 m B. 3 m C. 6 m D. -6 m
解析:首先审清题意,明确“正”和“负”所表示的意义,再根据题意作答.
答案:(1)B (2)A
点评:本题考查了正数和负数,解题关键是理解“正”和“负”的相对性,明确什么是一对具有相反意义的量.在一对具有相反意义的量中,先规定其中一个为正,则另一个就用负表示.
考点二 相反数、绝对值、倒数
例2 填空:
(1)(南京市中考)-2的相反数是________,-2的绝对值是________;

答案:(1)2 2 (2)3
点评:本题主要考查了相反数、绝对值、倒数的定义,要求熟练运用定义解题.
例3 (徐州市中考)点A,B,C在同一条数轴上,其中点A、B表示的数分别为-3、1,若BC=2,则AC等于( )
A. 3 B. 2 C. 3或5 D. 2或6
解析:本题利用数形结合思想,将A,B,C三点在数轴上表示后,即可计算AC的长.又因为题设条件点C的位置未知,故必须对此进行分类讨论,即点C在线段AB内或点C在线段AB外等两种情形.因为点A,B表示的数分别为-3、1,故AB=4.
当点C在线段AB外,如图1所示,AC=4+2=6;
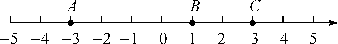 图1
图1当点C在线段AB内,如图所2示,AC=4-2=2.
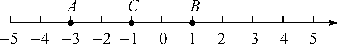 图2
图2答案:D
点评:根据绝对值的定义可知,在数轴上表示x1,x2的两个数的点A、B之间的距离公式是AB=

考点三 有理数的大小比较
例4 选择题:
(1)(扬州市中考)下列各数中,比-2小的数是( )
A. -3 B. -1 C. 0 D. 1
(2)(盐城市中考)-2,0,1,-3四个数中,最小的数是( )
A. -2 B. 0 C. 1 D. -3
解析:根据题意,结合实数大小的比较,从符号和绝对值两个方面分析可得答案.(1)比-2小的数应该是负数,且绝对值大于2的数,故只有A符合;(2)因为负数比正数和0小,故本题只要比较-2与-3的大小,因为<,故根据两个负数中绝对值较大的反而小,故选D.
答案:(1)A (2)D
点评:有理数的大小比较的步骤通常是首先判断正负数,再求其绝对值,最后比较得之.
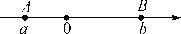
例5 (连云港市灌云县期末)如图,数轴上的点A,B分别对应实数a,b,下列结论中正确的是( )
A. a>b B. |a|>|b| C. -a<b D. a+b<0
解析:在数轴上,左边的点表示的数小于右边的点表示的数,由此判断选项正确与否.因为数a表示的点离原点比数b表示的点近,根据绝对值定义|a|<|b|,且a<0<b,即-a<b,故选C.
答案:C
点评:本题利用了数形结合思想判断得之,对于选择填空题,也可利用特殊值法判断,如本题可根据图取a=-1,b=2,从而得出选项C正确.
考点四 有理数的乘方与科学记数法
例8 填空:
(1)(镇江市枫叶国际学校期末)地震中里氏震级每增加1级,释放的能量增大到原来的32倍,那么里氏________级地震释放的能量是3级地震释放能量的324倍.
(2)(南通市中考)我国第一艘航母“辽宁舰”最大排水量为67500吨,这个数据用科学记数法可表示为__________________吨.
解析:(1)正确理解题意,若里氏1级地震释放的能量记为a,则里氏2级地震释放的能量为32a,里氏3级地震释放的能量为322a,依次类推,里氏3级地震释放能量的324倍,即为323-1·324=326,故里氏7级地震释放的能量是3级地震释放能量的324倍;(2)根据科学记数法的定义表示即可.
答案:(1)7 (2)6.75×104
点评:科学记数法的表示形式为a×10n,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.
考点五 有理数的混合运算
例9 (扬州市扬州中学期末)计算:
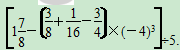 .
.解析:①式子的结构特点:本题为含有多重括号的混合运算问题,以及含有带分数和除法运算;②运算顺序:中括号内,先乘方,后乘法分配律(简便运算),再求差,最后求商;③按已确定的顺序,运用各级运算法则运算.
按照含有多重括号的运算顺序,应先计算小括号内的值,但是,根据本题的特点,若先利用乘法的分配律,则运算会简单得多.计算是还应注意将式子中带分数化为假分数,除法转化为乘法.

点评:为了确保运算的准确和快速,可采取步步为营的方法进行,有乘方先算乘方,再算乘除,最后算加减,切记不要“跳步”太多.
考点六 有理数的实际应用
例10 (淮安市清江中学期末)一辆货车从超市出发,向东走了1 km,到达小明家,继续向东走了3 km到达小兵家,然后向西走了10 km,到达小华家,最后又向东走了6 km结束行程.
(1)如果以超市为原点,以向东为正方向,用1个单位长度表示1 km,请你在如图所示的数轴上表示出小明家、小兵家和小华家的具体位置.
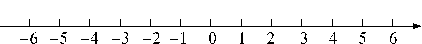
(2)请你通过计算说明货车最后回到什么地方?
(3)如果货车行驶1 km的用油量为0.25 L,请你计算货车从出发到结束行程共耗油多少升?
解析:(1)根据题意可知,小明家的位置在数1表示的点,小兵家的位置在数1+3=4表示的点,小华家的位置在数4-10=-6表示的点,从而标出各家位置;(2)由题意可知,货车行驶线路可用+1,+3,-10,+6等有理数来描述,从而计算它们的代数和,即可判断货车最后位置;(3)对货车行驶线路中的数据求它们的绝对值之和,即可计算总路程,再根据公式“耗油量=货车行驶每千米耗油量×货车行驶所走的总路程”计算得之.
答案:(1)小明家、小兵家和小华家在数轴上的位置如图所示:
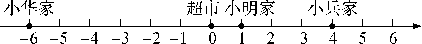
(2)由题意得(+1)+(+3)+(-10)+(+6)=0,因而货车回到了超市.
(3)由题意得1+3+10+6=20,货车从出发到结束行程共耗油:0.25×20=5(L),即货车从出发到结束行程共耗油5 L.
点评:有关有理数的实际应用问题,就是根据正负数的定义,对两个具有相反意义的量进行恰当的描述,再对这些数据或求代数和或求绝对值之和,从而解答问题.
考点七 数学思想与方法
例11 (扬州市高邮市期末改编)在数轴上,表示数m与n的点之间的距离可以表示为|m-n|.例如:在数轴上,表示数-3与2的点之间的距离是5=|-3-2|,表示数-4与-1的点之间的距离是3=|-4-(-1)|.利用上述结论解决如下问题:
(1)若|x-5|=3,求x的值;
(2)点A、B为数轴上的两个动点,点A表示的数是a,点B表示的数是b,且|a-b|=6(b>a),点C表示的数为-2,若A、B、C三点中的某一个点是另两个点组成的线段的中点,求a、b的值.
解析:本题含有数形结合及分类讨论的数学思想,首先利用绝对值的几何意义求解第(1)题,然后分类讨论点A、B、C的位置,解决第(2)问.
答案:(1)因为|x-5|=3,所以在数轴上,表示数x的点与数5的点之间的距离为3,所以x=8或x=2.
(2)因为|a-b|=6(b>a),所以在数轴上,点B与点A之间的距离为6,且点B在点A的右侧.
①当点C为线段AB的中点时,如图1所示,AC=BC=2AB=3.因为点C表示的数为-2,所以a=-2-3=-5,b=-2+3=1.
 图1
图1②当点A为线段BC的中点时,如图2所示,AC=AB=6.因为点C表示的数为-2,所以a=-2+6=4,b=a+6=10.
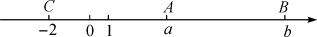 图2
图2③当点B为线段AC的中点时,如图3所示,BC=AB=6.因为点C表示的数为-2,所以b=-2-6=-8,a=b-6=-14.
综上,a=-5,b=1或a=4,b=10或a=-14,b=-8.
 图3
图3点评:绝对值的几何意义就是在数轴上表示的点到原点的距离,从而数轴上表示数x1,x2的两点间的距离公式是
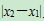 .
.临门一脚
本章引入了正、负数的概念,从而使数“扩张”到有理数,并将有理数在数轴上表示,定义了相反数、绝对值、倒数等概念,规定了有理数的加、减、乘、除、乘方运算法则,介绍了科学记数法.在本章的练习中,应掌握类比思想——将小学算术运算法则类比到有理数运算;数形结合思想——在数轴上理解绝对值的几何意义、比较有理数的大小;归纳猜想思想——运算规律与运算结果的探究.还有在有理数的运算过程中必须注意运算顺序:乘方、乘除、加减,如有括号,需先进行括号内运算或先去括号再运算.



发表评论 取消回复