代数式
知识回放

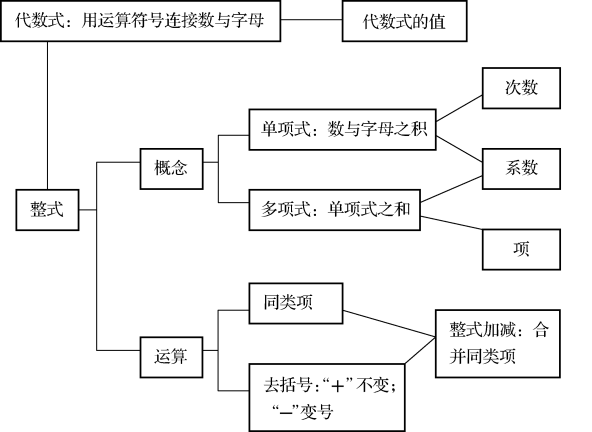
名师精讲
考点一 代数式的有关概念

考点二 同类项及合并同类项　
 
例2　(盐城市滨海县期末)填空：
(1)若单项式3x2yn与－2xmy3是同类项，则m＋n＝________；
(2)合并同类项：3c2－8c＋2c3－13c2＋2c－2c3＋3＝____________；0.5m2n－0.4mn2＋0.2nm2－0.8mn2＝__________________.
解析：(1)若两个单项式是同类项，则要求相同字母对应的指数相同，由此可得得出答案．即由条件得m＝2，n＝3，从而m＋n＝5.
(2)合并同类项法则是：字母和字母的指数不变，系数相加减．故原式＝(2c3－2c3)＋(3c2－13c2)＋(－8c＋2c)＋3＝－10c2－6c＋3；原式＝(0.5m2n＋0.2nm2)＋(－0.4mn2－0.8mn2)＝0.7m2n－1.2mn2.
答案：(1)5
(2)－10c2－6c＋3　0.7m2n－1.2mn2
点评：同类项的定义中强调，除所含字母相同外，相同字母的指数也要相同．其中，常数项也是同类项．合并同类项时，若不是同类项，则不需合并. 
考点三 去(添)括号　
 
例3　(泰州市第二中学附属初中期末)计算： 3x2－2(1－2x)－[5x2－(4x2－3x＋6)]．
解析：本题含有小括号与中括号，其运算顺序可以先去中括号再去小括号，也可先去小括号再去中括号，然后再合并同类项．
答案：解法1  原式＝3x2－2＋4x－(5x2－4x2＋3x－6)＝3x2＋4x－2－x2－3x＋6＝2x2＋x＋4.
解法2  原式＝3x2－2＋4x－5x2＋(4x2－3x＋6)＝－2x2＋4x－2＋4x2－3x＋6＝2x2＋x＋4.
点评：根据多重括号的去括号法则，可由里向外，也可由外向里逐层推进，在计算过程中要注意符号的变化．若括号前是“－”号，在去括号时，括号里各项都应变号；若括号前有数字因数，应把数字因数乘到括号里，再去括号
考点四 式的加减　
 
例4　(泰州市泰州中学附属初中期末)求比多项式5a2－2a－3ab＋b2少5a2－ab的多项式．
解析：本题是文字应用题，若A比B少C，则A－B＝C，从而B＝A－C，由此列式计算．
答案：依题意，列式为：(5a2－2a－3ab＋b2)－(5a2－ab)＝5a2－2a－3ab＋b2－5a2＋ab＝－2a－2ab＋b2.
点评：当整式是一个多项式，不是一个单项式时，应用括号把一个整式作为一个整体来加减．
考点五 化简求值　
 
例5　解答下列各题：
(1)(连云港市灌云县期末)已知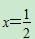(1)，y＝－1，求5(2x2y－3x)－2(4x－3x2y)的值．
(2)若3xm＋5y2与x3yn的和是单项式，则mn＝________.
(3)(苏州市张家港市期末)如果代数式5a＋3b的值为－4，那么代数式2(a＋b－1)＋4(2a＋b＋2)的值是多少？
解析：对于求代数式的值，常用先化简，后求值的概念，即先将复杂的代数式进行化简得到简单的代数式，然后代入值求出结果．对于第(2)题，由题意知3xm＋5y2和x3yn是同类项，所以m＋5＝3，n＝2，解得m＝－2，n＝2，所以mn＝(－2)2＝4.
答案：(1)5(2x2y－3x)－2(4x－3x2y)＝10x2y－15x－8x＋6x2y＝16x2y－23x.

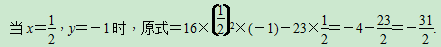
(2)4
(3)2(a＋b－1)＋4(2a＋b＋2)＝2a＋2b－2＋8a＋4b＋8＝10a＋6b＋6＝2(5a＋3b)＋6.
因为5a＋3b＝－4，所以原式＝2×(－4)＋6＝－2.
点评：有关代数式的求值问题，通常有三种考点：一是直接化简代入，二是条件求值，三是整体代入，其中整体代入的一般做法是对代数式先进行化简，然后找到化简结果与已知条件之间的联系．
考点六 代数式的实际应用　
 
例6　(苏州市张家港市期末)解答下列各题：
(1)某校艺术班同学，每人都会弹钢琴或古筝，其中会弹钢琴的人数比会弹古筝的人数多10人，两种都会的有7人．设会弹古筝的有m人，则该班同学共有________人(用含有m的代数式表示)；
(2)惠民新村分给小慧家一套价格为12万元的住房．按要求，需首期(第一年)付房款3万元，从第二年起，每年应付房款0.5万元与上一年剩余房款的利息的和．假设剩余房款年利率为0.4%，小慧列表推算如下：
 
 
若第n年小慧家仍需还款，则第n年应还款______________万元(n>1)．
解析：(1)本题可通过画图找到其中的数量关系，将会弹古筝的m人画在一个圆圈内，将会弹钢琴的(m＋10)人画在另一个圆圈内，两个圆圈的公共部分就是两种都会的7人，从而有m＋(m＋10)－7＝2m＋3.
(2)关键是要理解付款的方式，第一年还掉3万元后，第二年付0.5万元和剩下的9万元的利息，第三年还0.5万元和剩下的(9－0.5)万元的利息，第四年则要还0.5万元和剩下的(9－2×0.5)万元的利息……所以除了第一年以外，第n年都是要还0.5万元和剩下的[9－0.5(n－2)]万元的利息，可列式0.5＋[9－0.5(n－2)]×0.4%，化简可知第n年应还款(0.54－0.002n)万元．
答案：(1)(2m＋3)　(2)(0.54－0.002n)
点评：(1)本题考查了列代数式的问题，其中蕴含了集合的思想；(2)本题题材来源于现实生活中的购房问题，解题时要抓住以下几点：①理解生活背景；②要注意观察数字之间的规律；③类似问题往往与有理数的运算律结合在一起考查．
考点七 数学思想与方法　
 
循环，周期为3，所以a2 012＝4，a2 013＝2，a2 014＝1.
从而a7－a8＋a9－a10＋a11－a12＝0＋…＋a2 005－a2 006＋a2 007－a2 008＋a2 009－a2 010＝0，故原式＝a1＋a2＋a3＋a4＋a5＋a6＋0＋a2 011－a2 012＋a2 013－a2 014＝6－3＋16－8＋4－2＋0＋1－4＋2－1＝11.
答案：2　11
点评：本题含有归纳猜想的数学思想，关键是正确理解题意，读懂f(a)表示什么，从而计算得之．
临门一脚
本章内容是用字母将实际生活中的一类数据抽象成代数式，从而实现了思维上的一个质的飞跃，并从特殊到一般的认知过程，首先介绍了整式，必须理解单项式的系数与次数、多项式的项与次数、同类项的定义，掌握整式的加减运算法则．本章渗透的数学思想有：整体代换思想——代数式的求值，分类讨论思想——实际生活中代数式模型．在整式的加减运算中，必须注意去括号法则的灵活运用，特别是括号前带有“－”时，去括号时括号内各项均变号，同时注意同类项的判断．