一元一次方程
知识回放
名师精讲
考点一 等式与方程有关概念
例1 解答下列各题:
(1)(重庆市中考)已知关于x的方程2x+a-9=0的解是x=2,则a的值为( )
A. 2 B. 3 C. 4 D. 5

点评:已知条件中涉及方程的解,把方程的解代入原方程,转化为关于字母系数的方程进行求解,可把这种方法叫做“有解就代入”.
例2 (苏州市高新区期末)如图,“●、■、▲”分别表示三种不同的物体,已知前两架天平保持平衡,要使第三架也平衡,那么“?”处应放“■”的个数为( )
A. 5 B. 4
C. 3 D. 2
解析:根据天平仍然处于平衡状态是一个等量关系,而列出一元一次方程求解即可.设每个“●、■、▲”三种不同的物体的质量分别为x,y,z,则由图示可知2x=y+z,x+y=z,从而2x=y+(x+y),于是x=2y,z=3y,故x+z=5y,故选A.
答案:A
点评:天平问题,相当于一个等式,而等式性质有两个,本题利用了等式基本性质.
考点二 一元一次方程的解法

点评:(1)本题考查了一元一次方程的解法,熟练掌握运算法则是解答本题的关键;(2)解一元一次方程时,除了要掌握常规的解题步骤以外,有时还要注意观察方程的特点,寻找解题技巧,使解方程过程简洁明了.
考点三 列方程解应用题
例4 (无锡市中考)某文具店一支铅笔的售价为1.2元,一支圆珠笔的售价为2元.该店在“6·1儿童节”举行文具优惠售卖活动,铅笔按原价打8折出售,圆珠笔按原价打9折出售,结果两种笔共卖出60支,卖得金额87元.若设铅笔卖出x支,则依题意可列得的一元一次方程为( )
A. 1.2×0.8x+2×0.9(60+x)=87 B. 1.2×0.8x+2×0.9(60-x)=87
C. 2×0.9x+1.2×0.8(60+x)=87 D. 2×0.9x+1.2×0.8(60-x)=87
解析:设铅笔卖出x支,根据题意得出等量关系:x支铅笔的售价+(60-x)支圆珠笔的售价=87,据此列出方程即可.设铅笔卖出x支,由题意得1.2×0.8x+2×0.9(60-x)=87.故选B.
答案:B
点评:本题属于利润、打折问题.其数量关系是:商品的利润率= 商品进价
商品进价
例5 (盐城市亭湖新区实验学校期末)盐城某旅行社组织甲、乙两个旅游团分别到西安、北京旅游,已知这两个旅游团共有55人,甲旅游团的人数比乙旅游团的人数的2倍少5人,问甲、乙两个旅游团各有多少人?
解析:设乙旅游团的人数为x,再用x的代数式表示甲旅游团的人数,根据条件列方程求解即可.
答案:设乙旅游团的人数为x,则甲旅游团的人数为2x-5,
由题意得x+(2x-5)=55,
解得x=20,从而2x-5=35.
即甲旅游团有35人,乙旅游团有20人.
点评:本题属于和、差、倍、分问题.此问题中常用“多、少、大、小、几分之几”或“增加、减少、缩小”等词语体现等量关系,审题时要抓住关键词,确定标准量与比较量,并注意每个词的细微差别.基本方法是:以和倍差中的一种关系设未知数并表示其他量,选用余下的关系列出方程.
例6 (盐城市射阳县期末)用正方形硬纸板做三棱柱盒子,每个盒子由3个长方形侧面和2个正三角形底面组成,硬纸板以如图两种方法裁剪(裁剪后边角料不再利用).
A方法:剪6个侧面;
B方法:剪4个侧面和5个底面.
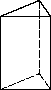
 A方法
A方法
 B方法
B方法
现有19张硬纸板,裁剪时x张用A方法,其余用B方法.
(1)用x的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
解析:根据条件“现有19张硬纸板”设裁剪时x张用A方法,则有(19-x)张用B方法,就可以分别表示出侧面个数和底面个数;由侧面个数和底面个数比为3∶2,根据裁剪出的侧面和底面个数相等建立方程,求出x的值,求出侧面的总数就可以求出结论.
答案:(1)因为裁剪时x张用A方法,所以裁剪时(19-x)张用B方法.
所以侧面的个数为6x+4(19-x)=2x+76,底面的个数为5(19-x)=(95-5x).
(2)由题意,得2(2x+76)=3(95-5x),解得x=7.
因此盒子的个数为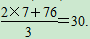 即裁剪出的侧面和底面恰好全部用完,能做30个盒子.
即裁剪出的侧面和底面恰好全部用完,能做30个盒子.
点评:本题属于几何图形类问题,仔细阅读后发现与鸡兔同笼类问题相同,又与倍分问题类似,第(2)小题的关键是确定“侧面个数和底面个数比为3∶2”.

点评:本题属于行程类问题,要掌握行程中的基本关系:路程=速度×时间.
相遇问题(相向而行),这类问题的等量关系是:各人走路之和等于总路程或同时走时两人所走的时间相等为等量关系.
追及问题(同向而行),这类问题的等量关系是:两人的路程差等于追及的路程或以追及时间为等量关系.
环形跑道上的相遇和追及问题,同地反向而行的等量关系是:两人走的路程和等于一圈的路程;同地同向而行的等量关系是:两人所走的路程差等于一圈的路程.
航(飞)行问题中的速度关系是:①顺水(风)速度=静水(无风)速度+水流(风)速度;②逆水速度=静水(无风)速度-水流(风)速度.

即这块水稻田的面积为36亩.
点评:本题属于工程类问题,其基本数量关系:工作总量=工作效率×工作时间;合做的效率=各单独做的效率的和.当工作总量未给出具体数量时,常设总工作量为“1”,分析时可采用列表或画图来帮助理解题意.
考点四 规律探究题
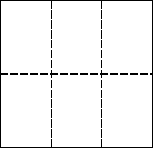
例9 一种长方形餐桌的四周可坐6 人用餐,现把若干张这样的餐桌按如图方式拼接.
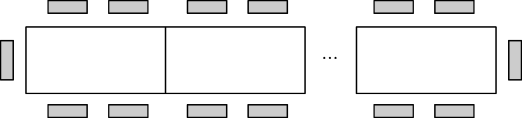
(1)若把4张、8张这样的餐桌拼接起来,四周分别可坐多少人?
(2)若用餐的人数有90人,则这样的餐桌需要多少张?
解析:(1)根据题意寻找规律,每增加1张这样的餐桌可增加4人求解即可;(2)根据寻找的规律,列一元一次方程求解即可.
答案:(1)寻找规律:1张这样的餐桌四周可坐6人,2张这样的餐桌拼接起来四周可坐(6+4)人,3张这样的餐桌拼接起来四周可坐(6+4×2)人,4张这样的餐桌拼接起来四周可坐(6+4×3)人……n张这样的餐桌拼接起来四周可坐[6+4(n-1)]人.
所以4张这样的餐桌拼接起来四周可坐:6+4×(4-1)=18(人),8张这样的餐桌拼接起来四周可坐:6+4×(8-1)=34(人).
(2)因为n张这样的餐桌拼接起来四周可坐[6+4(n-1)]人,所以若用餐的人数有90人,则有6+4(n-1)=90,
解得n=22.
即这样的餐桌需要22张.
点评:本题属于方案设计与规律探究题,关键是根据条件寻找规律,并由此列得方程,确定最佳方案.
例10 (苏州市青云中学期末)先观察,再解答.
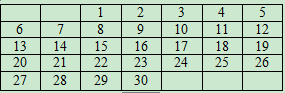
图1

图2
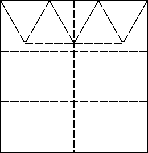
如图1是生活中常见的月历.
(1)如图2是另一个月的月历,a表示该月中某一天,b,c,d是该月中其他3天,b,c,d与a有什么关系?b=__________,c=__________,d=__________(用含a的式子填空);
(2)用一个长方形框圈出月历中的三个数字(如图2中的阴影),如果这三个数字之和等于51,这三个数字各是多少?
(3)这样圈出的三个数字的和可能是64吗?为什么?
解析:此题利用日历表中的数据特点“上下相邻日期相差7,左右相邻日期相差1”进行解答.
(1)b在a的上面,因此b=a-7;c在a的右面,因此c=a+1;a向前数两个即a-2,再向下便是d,即d=a-2+7=a-5;
(2)设中间数字为x,上面的数字为x-7,下面的数字为x+7,列方程解答即可;
(3)利用是否被3整除就可以判定.
答案:(1)a-7 a+1 a+5
(2)设中间的数字为x,上面的数字为x-7,下面的数字为x+7,
根据题意列方程得(x-7)+x+(x+7)=51,
解得x=17,
所以三个数字分别是10,17,24.
(3)不可能.理由是:这样圈出的三个数字的和是中间数字的3倍,64不能被3整除.
点评:本题属于数类问题,也是规律探究问题,这类方程的特点是,从给出的材料中找出规律,并利用这一规律找出解决问题的相等关系,列出方程.例如:数字排列规律,还有日历中的规律、年龄的规律、数字表示规律等.
考点五 数学思想与方法

点评:本题含有整体代换的数学思想.
例12 (南京市上元中学期末)已知某电脑公司有A型,B型,C型三种型号的电脑,其价格分别为A型每台6000元,B型每台4000元,C型每台2500元.我市某中学计划将100500元全部用于从该电脑公司购进其中两种不同型号的电脑共36台,请你设计出几种不同的购买方案供该校选择,并说明理由.
解析:本题条件中有三种型号的电脑,而要“购进其中两种不同型号的电脑”,因此必须对购进哪两种型号的电脑进行分类讨论.
答案:分三种情况考虑:
①购进A型电脑和B型电脑:
设购进A型电脑x台,则购进B型电脑(36-x)台,
由题意得6000x+4000(36-x)=100500.
解得x=-21.75,则36-x=57.75.不合题意,舍去;
②购进A型电脑和C型电脑:
设购进A型电脑x台,则购进C型电脑(36-x)台,
由题意得6000x+2 500(36-x)=100500.
解得x=3,则36-x=33;
③购进B型电脑和C型电脑:
设购进B型电脑y台,则购进C型电脑(36-y)台,
由题意得4000y+2 500(36-y)=100500.
解得y=7,则36-y=29.
所以有两种方案供该校选择,第一种方案是购进A型电脑3台和C型电脑33台;第二种方案是购进B型电脑7台和C型电脑29台.
点评:本题含有分类讨论的数学思想.
临门一脚
名师精讲
考点一 等式与方程有关概念
例1 解答下列各题:
(1)(重庆市中考)已知关于x的方程2x+a-9=0的解是x=2,则a的值为( )
A. 2 B. 3 C. 4 D. 5

点评:已知条件中涉及方程的解,把方程的解代入原方程,转化为关于字母系数的方程进行求解,可把这种方法叫做“有解就代入”.
例2 (苏州市高新区期末)如图,“●、■、▲”分别表示三种不同的物体,已知前两架天平保持平衡,要使第三架也平衡,那么“?”处应放“■”的个数为( )
A. 5 B. 4
C. 3 D. 2
解析:根据天平仍然处于平衡状态是一个等量关系,而列出一元一次方程求解即可.设每个“●、■、▲”三种不同的物体的质量分别为x,y,z,则由图示可知2x=y+z,x+y=z,从而2x=y+(x+y),于是x=2y,z=3y,故x+z=5y,故选A.
答案:A
点评:天平问题,相当于一个等式,而等式性质有两个,本题利用了等式基本性质.
考点二 一元一次方程的解法

点评:(1)本题考查了一元一次方程的解法,熟练掌握运算法则是解答本题的关键;(2)解一元一次方程时,除了要掌握常规的解题步骤以外,有时还要注意观察方程的特点,寻找解题技巧,使解方程过程简洁明了.
考点三 列方程解应用题
例4 (无锡市中考)某文具店一支铅笔的售价为1.2元,一支圆珠笔的售价为2元.该店在“6·1儿童节”举行文具优惠售卖活动,铅笔按原价打8折出售,圆珠笔按原价打9折出售,结果两种笔共卖出60支,卖得金额87元.若设铅笔卖出x支,则依题意可列得的一元一次方程为( )
A. 1.2×0.8x+2×0.9(60+x)=87 B. 1.2×0.8x+2×0.9(60-x)=87
C. 2×0.9x+1.2×0.8(60+x)=87 D. 2×0.9x+1.2×0.8(60-x)=87
解析:设铅笔卖出x支,根据题意得出等量关系:x支铅笔的售价+(60-x)支圆珠笔的售价=87,据此列出方程即可.设铅笔卖出x支,由题意得1.2×0.8x+2×0.9(60-x)=87.故选B.
答案:B
点评:本题属于利润、打折问题.其数量关系是:商品的利润率=
 商品进价
商品进价例5 (盐城市亭湖新区实验学校期末)盐城某旅行社组织甲、乙两个旅游团分别到西安、北京旅游,已知这两个旅游团共有55人,甲旅游团的人数比乙旅游团的人数的2倍少5人,问甲、乙两个旅游团各有多少人?
解析:设乙旅游团的人数为x,再用x的代数式表示甲旅游团的人数,根据条件列方程求解即可.
答案:设乙旅游团的人数为x,则甲旅游团的人数为2x-5,
由题意得x+(2x-5)=55,
解得x=20,从而2x-5=35.
即甲旅游团有35人,乙旅游团有20人.
点评:本题属于和、差、倍、分问题.此问题中常用“多、少、大、小、几分之几”或“增加、减少、缩小”等词语体现等量关系,审题时要抓住关键词,确定标准量与比较量,并注意每个词的细微差别.基本方法是:以和倍差中的一种关系设未知数并表示其他量,选用余下的关系列出方程.
例6 (盐城市射阳县期末)用正方形硬纸板做三棱柱盒子,每个盒子由3个长方形侧面和2个正三角形底面组成,硬纸板以如图两种方法裁剪(裁剪后边角料不再利用).
A方法:剪6个侧面;
B方法:剪4个侧面和5个底面.

 A方法
A方法 B方法
B方法现有19张硬纸板,裁剪时x张用A方法,其余用B方法.
(1)用x的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
解析:根据条件“现有19张硬纸板”设裁剪时x张用A方法,则有(19-x)张用B方法,就可以分别表示出侧面个数和底面个数;由侧面个数和底面个数比为3∶2,根据裁剪出的侧面和底面个数相等建立方程,求出x的值,求出侧面的总数就可以求出结论.
答案:(1)因为裁剪时x张用A方法,所以裁剪时(19-x)张用B方法.
所以侧面的个数为6x+4(19-x)=2x+76,底面的个数为5(19-x)=(95-5x).
(2)由题意,得2(2x+76)=3(95-5x),解得x=7.
因此盒子的个数为
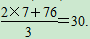 即裁剪出的侧面和底面恰好全部用完,能做30个盒子.
即裁剪出的侧面和底面恰好全部用完,能做30个盒子.点评:本题属于几何图形类问题,仔细阅读后发现与鸡兔同笼类问题相同,又与倍分问题类似,第(2)小题的关键是确定“侧面个数和底面个数比为3∶2”.

点评:本题属于行程类问题,要掌握行程中的基本关系:路程=速度×时间.
相遇问题(相向而行),这类问题的等量关系是:各人走路之和等于总路程或同时走时两人所走的时间相等为等量关系.
追及问题(同向而行),这类问题的等量关系是:两人的路程差等于追及的路程或以追及时间为等量关系.
环形跑道上的相遇和追及问题,同地反向而行的等量关系是:两人走的路程和等于一圈的路程;同地同向而行的等量关系是:两人所走的路程差等于一圈的路程.
航(飞)行问题中的速度关系是:①顺水(风)速度=静水(无风)速度+水流(风)速度;②逆水速度=静水(无风)速度-水流(风)速度.

即这块水稻田的面积为36亩.
点评:本题属于工程类问题,其基本数量关系:工作总量=工作效率×工作时间;合做的效率=各单独做的效率的和.当工作总量未给出具体数量时,常设总工作量为“1”,分析时可采用列表或画图来帮助理解题意.
考点四 规律探究题
例9 一种长方形餐桌的四周可坐6 人用餐,现把若干张这样的餐桌按如图方式拼接.

(1)若把4张、8张这样的餐桌拼接起来,四周分别可坐多少人?
(2)若用餐的人数有90人,则这样的餐桌需要多少张?
解析:(1)根据题意寻找规律,每增加1张这样的餐桌可增加4人求解即可;(2)根据寻找的规律,列一元一次方程求解即可.
答案:(1)寻找规律:1张这样的餐桌四周可坐6人,2张这样的餐桌拼接起来四周可坐(6+4)人,3张这样的餐桌拼接起来四周可坐(6+4×2)人,4张这样的餐桌拼接起来四周可坐(6+4×3)人……n张这样的餐桌拼接起来四周可坐[6+4(n-1)]人.
所以4张这样的餐桌拼接起来四周可坐:6+4×(4-1)=18(人),8张这样的餐桌拼接起来四周可坐:6+4×(8-1)=34(人).
(2)因为n张这样的餐桌拼接起来四周可坐[6+4(n-1)]人,所以若用餐的人数有90人,则有6+4(n-1)=90,
解得n=22.
即这样的餐桌需要22张.
点评:本题属于方案设计与规律探究题,关键是根据条件寻找规律,并由此列得方程,确定最佳方案.
例10 (苏州市青云中学期末)先观察,再解答.

图1

图2
如图1是生活中常见的月历.
(1)如图2是另一个月的月历,a表示该月中某一天,b,c,d是该月中其他3天,b,c,d与a有什么关系?b=__________,c=__________,d=__________(用含a的式子填空);
(2)用一个长方形框圈出月历中的三个数字(如图2中的阴影),如果这三个数字之和等于51,这三个数字各是多少?
(3)这样圈出的三个数字的和可能是64吗?为什么?
解析:此题利用日历表中的数据特点“上下相邻日期相差7,左右相邻日期相差1”进行解答.
(1)b在a的上面,因此b=a-7;c在a的右面,因此c=a+1;a向前数两个即a-2,再向下便是d,即d=a-2+7=a-5;
(2)设中间数字为x,上面的数字为x-7,下面的数字为x+7,列方程解答即可;
(3)利用是否被3整除就可以判定.
答案:(1)a-7 a+1 a+5
(2)设中间的数字为x,上面的数字为x-7,下面的数字为x+7,
根据题意列方程得(x-7)+x+(x+7)=51,
解得x=17,
所以三个数字分别是10,17,24.
(3)不可能.理由是:这样圈出的三个数字的和是中间数字的3倍,64不能被3整除.
点评:本题属于数类问题,也是规律探究问题,这类方程的特点是,从给出的材料中找出规律,并利用这一规律找出解决问题的相等关系,列出方程.例如:数字排列规律,还有日历中的规律、年龄的规律、数字表示规律等.
考点五 数学思想与方法

点评:本题含有整体代换的数学思想.
例12 (南京市上元中学期末)已知某电脑公司有A型,B型,C型三种型号的电脑,其价格分别为A型每台6000元,B型每台4000元,C型每台2500元.我市某中学计划将100500元全部用于从该电脑公司购进其中两种不同型号的电脑共36台,请你设计出几种不同的购买方案供该校选择,并说明理由.
解析:本题条件中有三种型号的电脑,而要“购进其中两种不同型号的电脑”,因此必须对购进哪两种型号的电脑进行分类讨论.
答案:分三种情况考虑:
①购进A型电脑和B型电脑:
设购进A型电脑x台,则购进B型电脑(36-x)台,
由题意得6000x+4000(36-x)=100500.
解得x=-21.75,则36-x=57.75.不合题意,舍去;
②购进A型电脑和C型电脑:
设购进A型电脑x台,则购进C型电脑(36-x)台,
由题意得6000x+2 500(36-x)=100500.
解得x=3,则36-x=33;
③购进B型电脑和C型电脑:
设购进B型电脑y台,则购进C型电脑(36-y)台,
由题意得4000y+2 500(36-y)=100500.
解得y=7,则36-y=29.
所以有两种方案供该校选择,第一种方案是购进A型电脑3台和C型电脑33台;第二种方案是购进B型电脑7台和C型电脑29台.
点评:本题含有分类讨论的数学思想.
本章内容从列代数式到列方程并求解,是学生数学思维的第二次飞跃,再从方程中的最简方程——一元一次方程开始学习,理解“方程的解”的定义,根据等式性质掌握“解方程”的一般步骤,并由此解决实际问题.本章知识中蕴涵的数学思想方法主要是问题解决中的化归思想——所有的一元一次方程通过适当的变形,都可以化为“x=a(a为已知数)”的形式,建立方程模型的思想——把一般的实际问题转化为数学问题,用数学的方法去解决.在解方程时必须注意每步变形的合理性,对于实际问题要考虑所得的解是否符合其实际意义.



发表评论 取消回复