走进图形世界
知识回放
名师精讲
考点一 空间几何体

名师精讲
考点一 空间几何体
例1 选择题:
(1)(泰州市泰州中学附属初中期末)如图,下列四个几何体中,它们各自从三个不同方向看得到的图形有两个相同,而另一个不同的几何体是( )
A. ①② B. ②③ C. ②④ D. ③④
(2)(宁波市中考)下列四张正方形硬纸片,剪去阴影部分后,如果沿虚线折叠,可以围成一个封闭的长方体包装盒的是( )
解析:(1)通过观察几何体,可以得到从三个方向看所得的图形,找出其中只有两个相同,另一个不同的几何体.正方体的三视图均为正方形;圆柱的三视图为两个长方形和一个圆;圆锥的三视图为两个三角形和一个圆;球的三视图均为圆.故选B.
(2)严格按照图中的方法亲自动手操作一下,即可很直观地呈现出来.A项,图剪去阴影部分后,组成无盖的正方体,故此选项不合题意;B项,图剪去阴影部分后,无法组成长方体,故此选项不合题意;C项,图剪去阴影部分后,能组成长方体,故此选项正确;D项,图剪去阴影部分后,组成无盖的正方体,故此选项不合题意.故选C.
答案:(1)B (2)C
点评:(1)由图得出每个图从不同方向所看得到的图形,再按条件得出答案;(2)做题时可亲自动手操作一下,增强空间想象能力.
考点二 直线、射线、线段
例2 (苏州市青云中学期末)在直线l上任取一点A,截取AB=16 cm,再截取AC=40 cm,求AB的中点D与AC的中点E的距离.
答案:①当C在AB的延长线上时,如图.
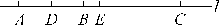
因为D是AB的中点,AB=16 cm,所以AD=2=2×16=8(cm).
因为E是AC的中点,AC=40 cm,所以AE=2AC=2×40=20(cm).
所以DE=AE-AD=20-8=12(cm);
②当C在BA的延长线上时,如图.

由①知AD=8 cm,AE=20 cm.
所以DE=AE+AD=20+8=28(cm).
所以D点与E点的距离是12 cm或28 cm.
点评:对于线段的和、差关系以及线段的中点问题的计算,需结合图形,认真观察分析.若已知线段上给出的点未明确其位置,还需要分类讨论,千万不要漏解.
考点三 角的计算
例3 填空:
(1)(镇江市天王中学期末)把15°30′化成度的形式,则15°30′=________;
(2)(常熟市外国语学校期末)一个角是25°42′,则它的余角为________.
解析:(1)将30′化成度数即可,因为30′=0.5°,所以15°30′=15.5°;(2)利用余角定义计算得之,即余角为90°-25°42′=64°18′.
答案:(1)15.5° (2)64°18′
例4 (泰州市第二中学附属初中期末)已知∠A和∠B互为余角,∠A与∠C互为补角,∠B和∠C的和等于周角的3.求∠A+∠B+∠C的度数.
解析:设∠A=x,再根据条件用含x的代数式表示∠B和∠C,从而列出方程求解即可,这是几何计算题的通法.
答案:设∠A=x,依题意∠B=90°-x,∠C=180°-x.
由∠B和∠C的和等于周角的3,得(90°-x)+(180°-x)=3×360°.
解得x=75°,所以∠B=90°-x=15°,∠C=180°-x=105°,
所以∠A+∠B+∠C=75°+15°+105°=195°.
点评:巧用方程求解余角、补角问题时,应注意:①正确设未知数并用含所设未知数的式子表示出相关的量:一般设某个角为x,根据余角、补角定义,则这个角的余角为90°-x,这个角的补角为180°-x;②依据已知条件,寻找出正确的相等关系,列出方程.
考点四 相交线与垂线
例5 (泰州市泰州中学附属初中期末)如图,直线AB,CD相交于点O,OE⊥AB于点O,OF平分∠AOE,∠1=15°30′,则下列结论中不正确的是( )
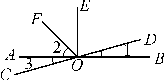
A. ∠2=45° B. ∠1=∠3
C. ∠AOD与∠1互为补角 D. ∠1的余角等于75°30′
解析:利用两直线互相垂直的性质得∠2=2∠AOE=45°,故A正确;根据对顶角性质,则B正确;根据邻补角定义,则C正确;根据互为余角的定义知90°-∠1=90°-15°30′=74°30′,故D不正确.故选D.
答案:D
点评:有关图形中的角的计算问题,首先要从图形中读出具有度量关系的角,如互余、互补、对顶角等,然后合理利用相关的定义、性质求解.
例6 (盐城市阜宁县期末)如图,直线AB、CD相交于点O,若∠BOD=40°,OA平分∠COE,则∠AOE=________.
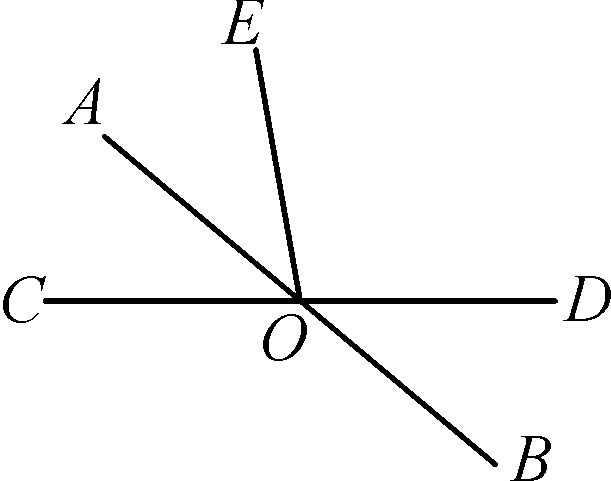
解析:根据对顶角相等求出∠AOC,再根据角平分线的定义解答.
因为∠BOD=40°,所以∠AOC=∠BOD=40°.因为OA平分∠COE,所以∠AOE=∠AOC=40°.故答案为40°.
答案:40°
点评:本题考查了对顶角相等的性质,角平分线的定义,是基础题,熟记性质并准确识图是解题的关键.
考点五 几何图形的实际应用
例7 (镇江市枫叶国际学校期末)如图,上下底面为全等的正六边形礼盒,其从正面看得到的图与从侧面看得到的图均由长方形构成,从正面看得到的图中大长方形边长如图所示,从侧面看得到的图中包含两个相同的长方形,如果用彩色胶带如图包扎礼盒,所需胶带长度至少为( )
A. 320 cm B. 395.24 cm C. 431.76 cm D. 480 cm
解析:从条件可知,侧面的每条胶带的长均为20 cm,其和为120 cm;上下面的每条胶带的长均小于60 cm,但大于50 cm,其和小于360 cm且大于300 cm,所以胶带总长在420 cm与480 cm之间,故选C.
答案:C
点评:本题考查几何体从不同的方向看得到的图形及正多边形的有关计算,解题时要根据视图中的数据计算几何体中的相关内容.
考点六 数学思想与方法
例8 (江阴市射阳县期末)小明在看书时发现这样一个问题: “ 在某次聚会中,共有6人参加,如果每两人都握一次手,共握几次手?” 小明通过认真思考得出了答案,为了解决更一般的问题,小明设计了下列图表进行探究:
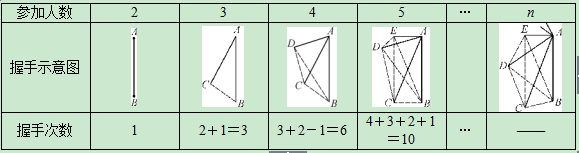
请你在上表右下角的横线上填上你归纳出的一般结论.

(3)与此类比可得有关角的计数结论.
点评:本题蕴含数形结合、归纳猜想等数学思想,将握手问题转化为研究直线上的点构成线段的条数问题. 这里,视一个人为直线上的一个点,通过仔细观察图表,探究推理可得问题的答案.
例8 (苏州市张家港市期末)如图,直线l上有A,B两点,AB=12 cm,点O是线段AB上的一点,OA=2OB.

(1)OA=________cm,OB=________cm;
(2)若点C是线段AB上一点,且满足AC=CO+CB,求CO的长;
(3)若动点P,Q分别从点A,B同时出发,向右运动,点P的速度为2 cm/s,点Q的速度为1 cm/s,设运动时间为t s.当点P与点Q重合时,P、Q两点停止运动.
①当t为何值时,2OP-OQ=4?
②当点P经过点O时,动点M从点O出发,以3 cm/s的速度也向右运动.当点M追上点Q后立即返回,以3 cm/s的速度向点P运动,遇到点P后再立即返回,以3 cm/s的速度向点Q运动,如此往返,直到点P,Q停止时,点M也停止运动.在此过程中,点M行驶的总路程是多少?
解析:第(1)题,根据条件直接求解;第(2)题,因为点C的位置不确定,故需要分类讨论,即考虑点C在线段AO上或在线段OB上;第(3)题,用含t的代数式表示OP与OQ的长度,但也要分类讨论,从而根据条件列方程,解之即可解决第①题;第②题属于行程类应用题,先求时间,再求路程.
答案:(1)8 4
(2)设CO=x cm.
当点C在线段AO上时(如图1),
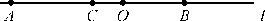 图1
图1则AC=(8-x)cm,CB=(4+x)cm.
由AC=CO+CB,得8-x=x+4+x,解得x=3;
当点C的线段OB上时(如图2),
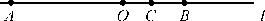 图2
图2则AC=(8+x)cm,CB=(4-x)cm.
由AC=CO+CB,得8+x=x+4-x,解得x=-4(舍去).
综上所述,CO的长为3 cm.
(3)①当点P在点O的左侧时(如图3),
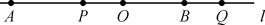 图3
图3则OP=(8-2t)cm,OQ=(4+t)cm.
由2(8-2t)-(4+t)=4,解得t=5;
当点P在点O的右侧时(如图4),
 图4
图4则OP=(2t-8)cm,OQ=(4+t)cm.
由2(2t-8)-(4+t)=4,解得t=8.
综上所述,当t=5或t=8时,2OP-OQ=4.
②AO=8 cm,点P从点A运动到点O的时间t=8÷2=4(s),则点M运动的时间为:(4+4×1)÷(2-1)=8(s),因此点M运动的总路程为3×8=24(cm).
点评:有关几何计算题,主要利用方程思想求解长度或角度,当含有位置关系时,需进行分类讨论.
例9 (北京市中考)

如图,∠DOE=50°,OD平分∠AOC,∠AOC=60°,OE平分∠BOC.
(1)用直尺、量角器画出射线OA,OB,OC的准确位置;
(2)求∠BOC的度数,要求写出计算过程;
(3)当∠DOE=α,∠AOC=2β时(其中0°<β<α,0°<α+β<90°),用α,β的代数式表示∠BOC的度数.(直接写出结果即可)
解析:本题含有分类讨论的数学思想,因角是由两条公共端点的射线组成的,而射线的位置没有确定,故需考虑射线OA,OB,OC的不同位置情形.
答案:(1)①当射线OA在∠DOE外部时,射线OA,OB,OC的位置如图1所示.
②当射线OA在∠DOE内部时,射线OA,OB,OC的位置如图2所示.
(2)①当射线OA在∠DOE外部时,此时射线OC在∠DOE内部,射线OA,OD,OC,OE,OB依次排列,如图1.
因为OD平分∠AOC,∠AOC=60°,所以∠DOC=
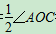 ∠AOC=30°.
∠AOC=30°.因为此时射线OA,OD,OC,OE,OB依次排列,所以∠DOE=∠DOC+∠COE.
因为∠DOE=50°,所以∠COE=∠DOE-∠DOC=50°-30°=20°.
因为OE平分∠BOC,所以∠BOC=2∠COE=2×20°=40°;
②当射线OA在∠DOE内部时,此时射线OC在∠DOE外部,射线OC,OD,OA,OE,OB依次排列,如图2.
因为OD平分∠AOC,∠AOC=60°,所以∠COD=
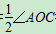 ∠AOC=30°.
∠AOC=30°.因为此时射线OC,OD,OA,OE,OB依次排列,∠DOE=50°,所以∠COE=∠COD+∠DOE=30°+50°=80°.
因为OE平分∠BOC,所以∠BOC=2∠COE=2×80°=160°.
(3)当射线OA在∠DOE外部时,∠BOC=2α-2β;当射线OA在∠DOE内部时,∠BOC=2α+2β.
点评:分类讨论是重要的数学思想,在中学数学的各个知识点,均有可能出现,必须引起重视.
临门一脚
本章内容包括立体图形与平面图形两部分内容,从“几何模型→图形→文字→符号”这个抽象的过程,培养空间想象能力和逻辑推理能力,通过观察、思考、探究等活动归纳出图形的概念和性质,还要说出理由,把它作为通过实验探究得到结论的自然延续.在说理时,必须注意“理”有根有据,即必须根据教材所给的重要结论来说明道理.在线段与角的相关计算与证明中,还要注意方程思想与分类讨论思想的应用.



发表评论 取消回复