函数的应用
一、 重点知识及常用结论
一、 重点知识及常用结论
1. 函数的零点
(1)三个等价关系
方程f(x)=0有实数根⇔函数y=f(x)的图像与x轴有交点⇔函数y=f(x)有零点.
(2)函数零点的判定(零点存在性定理)
如果函数y=f(x)在区间[a,b]上的图像是一条连续不断的曲线,并且有f(a)·f(b)<0,那么函数y=f(x)在区间(a,b)内有零点.
2. 二分法
对于在区间[a,b]上连续且f(a)·f(b)<0的函数y=f(x),通过不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法.
3. 二次函数y=ax2+bx+c (a>0)的图像与零点的关系
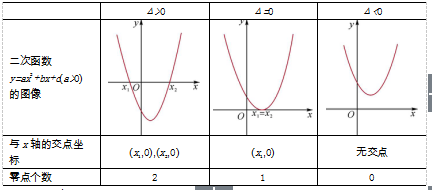
点拨:有关函数零点的结论:
(1)三个等价关系
方程f(x)=0有实数根⇔函数y=f(x)的图像与x轴有交点⇔函数y=f(x)有零点.
(2)函数零点的判定(零点存在性定理)
如果函数y=f(x)在区间[a,b]上的图像是一条连续不断的曲线,并且有f(a)·f(b)<0,那么函数y=f(x)在区间(a,b)内有零点.
2. 二分法
对于在区间[a,b]上连续且f(a)·f(b)<0的函数y=f(x),通过不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法.
3. 二次函数y=ax2+bx+c (a>0)的图像与零点的关系

点拨:有关函数零点的结论:
(1)若连续函数f(x)在定义域上是单调函数,则f(x)至多有一个零点.
(2)连续函数相邻两个零点之间的所有函数值保持同号.
(3)连续函数图像通过零点时,函数值可能变号,也可能不变号.
二、 典型例题及易错题型
对于函数的应用问题,一方面要熟练地掌握相关函数的性质,另一方面,要将所学习的相关知识进行有效地融合在一起进行思考问题,同时,要充分应用好相关的数学思想,如数形结合思想、分类讨论思想、方程与函数思想、转化与化归思想等来将问题进行直观化、简单化,从而达到快速、有效地解题的目的.
例 (2018浙江名校协作体)已知函数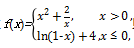 则关于x的方程f(x2-4x)=6的不同实根的个数为 .
则关于x的方程f(x2-4x)=6的不同实根的个数为 .
答案:4 解析:作出函数f(x)的图像如图所示,t=x2-4x=(x-2)2-4,由图可知,当-4≤t≤0时,f(t)=6无解,当t>0时,f(t)=6有2个解,对应t=x2-4x,各有2个解,故关于x的方程f(x2-4x)=6的不同实根的个数为4.
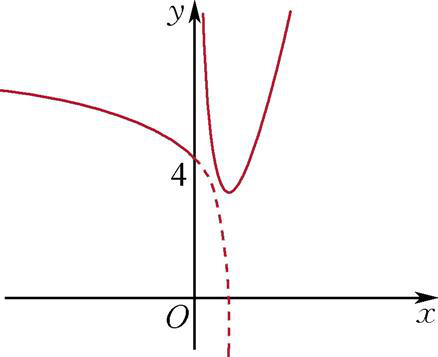
方法突破:对于复合函数的零点问题,通常是将复合函数转化为基本初等函数来加以研究,借助于基本初等函数的图像,达到将复杂问题简单化,将抽象问题具体化,实现化难为易,化繁为简的目的。
(2)连续函数相邻两个零点之间的所有函数值保持同号.
(3)连续函数图像通过零点时,函数值可能变号,也可能不变号.
二、 典型例题及易错题型
对于函数的应用问题,一方面要熟练地掌握相关函数的性质,另一方面,要将所学习的相关知识进行有效地融合在一起进行思考问题,同时,要充分应用好相关的数学思想,如数形结合思想、分类讨论思想、方程与函数思想、转化与化归思想等来将问题进行直观化、简单化,从而达到快速、有效地解题的目的.
例 (2018浙江名校协作体)已知函数
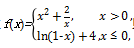 则关于x的方程f(x2-4x)=6的不同实根的个数为 .
则关于x的方程f(x2-4x)=6的不同实根的个数为 . 答案:4 解析:作出函数f(x)的图像如图所示,t=x2-4x=(x-2)2-4,由图可知,当-4≤t≤0时,f(t)=6无解,当t>0时,f(t)=6有2个解,对应t=x2-4x,各有2个解,故关于x的方程f(x2-4x)=6的不同实根的个数为4.

方法突破:对于复合函数的零点问题,通常是将复合函数转化为基本初等函数来加以研究,借助于基本初等函数的图像,达到将复杂问题简单化,将抽象问题具体化,实现化难为易,化繁为简的目的。



发表评论 取消回复